Könnte jemand mir Ameisenalgorithmen erklären und sagen, was wäre hier ein optimaler Pfad?
PS: Die rote Felder darf man nicht betreten.
Danke im Voraus
Ist rot eine Barriere?
ja, das Betreten der roten Felder ist verboten.
Eigentlich sind’s zwei Probleme, kürzeste „Linie“ zwischen jeweils zwei Punkten finden, und TSP. Ich denke, dabei bei können dir hier auch andere helfen.
Zum Einlesen in den Aufgabeteil 1: Count paths with distance equal to Manhattan distance - GeeksforGeeks
Aufgabenteil 2 ist das TSP. Was hast du bis jetzt und woran „zwickt“ es noch ein bisschen?
Ich finde es übrigens sehr schade, dass dir kein anderer antworten möchte… 
Etwas OT:
Wenn die „Frage“ mehr wäre als ein Screenshot von einer Aufgabenstellung und der Aufforderung: „Liefert mir (gefälligst) die Lösung, und erklärt sie mir auch“, dann wäre das was anderes. Umgekehrt könnte man argumentieren, dass eine Antwort mit dem Inhalt „Hier schau mal ein Link den ich gerade schnell zu diesem Thema ergooglet habe“ auch nicht das ist, was ich mir hier (für ein Forum) wünschen würde. Aber in bezug auf … sagen wir mal „Engagement“ oder „Tiefe der Unterhaltung“ … passt das zumindest zusammen ![]()
Ich habe hier ein paar Beiträge gelöscht.
@Adriano10 : Wenn du eine vernünftige, konstruktive, fachlich fundierte Antwort erwartest, dann kannst du die definitiv hier bekommen. Aber dann musst du deine Frage auch entsprechend formulieren.
Was das ungefähr bedeutet, weißt du, und wenn du es nicht weißt, liegt dein größtes Problem nicht darin, dass du die Antwort auf eine Frage finden musst.
Für den Anfang sollte es reichen, wenn ich sage: Gib’ dir Mühe.
@CyborgBeta I’m watching you…
Das müsste eigentlich der Ameisenalgorithmus sein, wenn nicht noch grobe Schnitzer dabei sind. Auf jedem Punkt starten 100 Ameisen:
import java.awt.Point;
import java.util.Comparator;
import java.util.Iterator;
import java.util.LinkedList;
import java.util.List;
import java.util.Random;
import java.util.stream.Collectors;
public class ShortestPath {
private static Point getLast(List<Point> path) {
return path.get(path.size() - 1);
}
private static void printPath(List<Point> path) {
System.out.println(path.stream().map(p -> "(" + p.x + "," + p.y + ")").collect(Collectors.joining("->")));
}
public static void main(String[] args) {
// the graph
int[][] graph = new int[7][7];
graph[1][1] = 3;
graph[1][2] = 1;
graph[1][3] = 2;
graph[3][3] = 1;
graph[3][4] = 1;
graph[4][4] = 5;
graph[5][3] = 1;
graph[6][0] = 4;
// the end points
List<Point> nodes = new LinkedList<Point>();
nodes.add(new Point(3, 1));
nodes.add(new Point(1, 1));
nodes.add(new Point(0, 6));
nodes.add(new Point(4, 4));
// the ants
List<Ant> ants = new LinkedList<Ant>();
for (Point point : nodes) {
for (int i = 0; i < 100; i++) {
ants.add(new Ant(point));
}
}
// moves...
for (int i = 0; i < 100; i++) {
for (Ant ant : ants) {
ant.next(graph);
}
}
// remove
for (Iterator<Ant> iterator = ants.iterator(); iterator.hasNext();) {
Ant ant = iterator.next();
if (ant.alive) {
iterator.remove();
}
}
// sort
ants.sort(new Comparator<Ant>() {
public int compare(Ant a1, Ant a2) {
return a1.path.size() - a2.path.size();
}
});
// the TSP 1
List<List<Point>> tsp = new LinkedList<List<Point>>();
a: for (Ant ant : ants) {
List<Point> path = ant.path;
for (List<Point> list : tsp) {
if (path.get(0).equals(list.get(0)) && getLast(path).equals(getLast(list))) {
continue a;
}
}
tsp.add(path);
}
// the TSP 2
List<Point> visited = new LinkedList<Point>();
List<Point> path = tsp.remove(0);
visited.add(getLast(path));
printPath(path);
while (visited.size() < nodes.size()) {
for (List<Point> list : tsp) {
if (getLast(path).equals(list.get(0)) && !visited.contains(getLast(list))) {
visited.add(getLast(list));
path = list;
break;
}
}
printPath(path);
}
}
}
class Ant {
static Random random = new Random(1);
static float dirProbability = 0.1f;
Point xy;
int dirx;
int diry;
List<Point> path = new LinkedList<Point>();
boolean alive = true;
Ant(Point p) {
xy = p;
setDir();
path.add(p);
}
void setDir() {
if (random.nextInt(2) == 0) {
dirx = random.nextInt(2) == 0 ? -1 : +1;
diry = 0;
} else {
dirx = 0;
diry = random.nextInt(2) == 0 ? -1 : +1;
}
}
void setAlive(int[][] graph) {
Point start = path.get(0);
Point end = xy;
if (graph[end.y][end.x] > 1 && !start.equals(end)) {
alive = false;
}
}
void next(int[][] graph) {
if (alive) {
Point p = new Point(xy.x + dirx, xy.y + diry);
if (!check(graph, p) || random.nextFloat() < dirProbability) {
do {
setDir();
p = new Point(xy.x + dirx, xy.y + diry);
} while (!check(graph, p));
}
xy = p;
path.add(p);
setAlive(graph);
}
}
boolean check(int[][] graph, Point p) {
if (p.x < 0 || p.y < 0 || p.x >= graph.length || p.y >= graph.length) {
return false;
}
if (graph[p.y][p.x] == 1) {
return false;
}
return true;
}
}
Man muss denke ich bei TSP 2 zu Beginn den Anfangspunkt auch noch hinzufügen - wenn man das mit 1000 Ameisen pro Punkt ausprobiert, dann fällt das auf.
„Optimale Lösung…“ kann ich nicht genau sagen, der Ameisenalgorithmus ist ja quasi nur eine intelligente Heuristik.
Hab es nochmal etwas geändert:
import java.util.HashSet;
import java.util.LinkedList;
import java.util.List;
import java.util.Objects;
import java.util.Random;
import java.util.stream.Collectors;
public class ShortestPath {
private static Point getLast(List<Point> path) {
return path.get(path.size() - 1);
}
private static void printPath(List<Point> path) {
System.out.println(path.stream().map(p -> "(" + p.x + "," + p.y + ")").collect(Collectors.joining("->")));
}
public static void main(String[] args) {
// the graph
int[][] graph = new int[7][7];
graph[1][1] = 3;
graph[1][2] = 1;
graph[1][3] = 2;
graph[3][3] = 1;
graph[3][4] = 1;
graph[4][4] = 5;
graph[5][3] = 1;
graph[6][0] = 4;
// the end points
List<Point> nodes = new LinkedList<Point>();
nodes.add(new Point(3, 1));
nodes.add(new Point(1, 1));
nodes.add(new Point(0, 6));
nodes.add(new Point(4, 4));
// the ants
List<Ant> ants = new LinkedList<Ant>();
for (Point point : nodes) {
for (int i = 0; i < 10000; i++) {
ants.add(new Ant(point));
}
}
// moves...
for (int i = 0; i < 100; i++) {
for (Ant ant : ants) {
ant.next(graph);
}
}
// the TSP
List<List<Point>> tsp = ants.stream().filter(a -> !a.alive).sorted((a1, a2) -> a1.path.size() - a2.path.size())
.distinct().map(a -> a.path).collect(Collectors.toList());
// the TSP 2
List<List<Point>> tsp2 = new LinkedList<List<Point>>();
HashSet<Point> visited = new HashSet<Point>();
List<Point> first = tsp.get(0);
tsp2.add(first);
visited.add(first.get(0));
visited.add(getLast(first));
while (visited.size() < nodes.size()) {
for (List<Point> list : tsp) {
if (!visited.contains(getLast(list)) && getLast(first).equals(list.get(0))) {
tsp2.add(list);
visited.add(getLast(list));
first = list;
}
}
}
visited.remove(tsp.get(0).get(0));
for (List<Point> list : tsp) {
if (!visited.contains(getLast(list)) && getLast(first).equals(list.get(0))) {
tsp2.add(list);
visited.add(getLast(list));
first = list;
}
}
for (List<Point> list : tsp2) {
printPath(list);
}
// Frame.show(graph, tsp2);
}
}
class Ant {
static Random random = new Random(1);
static float dirProbability = 0.1f;
Point xy;
int dirx;
int diry;
List<Point> path = new LinkedList<Point>();
boolean alive = true;
Ant(Point p) {
xy = p;
setDir();
path.add(p);
}
void setDir() {
if (random.nextInt(2) == 0) {
dirx = random.nextInt(2) == 0 ? -1 : +1;
diry = 0;
} else {
dirx = 0;
diry = random.nextInt(2) == 0 ? -1 : +1;
}
}
void setAlive(int[][] graph) {
Point start = path.get(0);
Point end = xy;
if (graph[end.y][end.x] > 1 && !start.equals(end)) {
alive = false;
}
}
void next(int[][] graph) {
if (alive) {
Point p = new Point(xy.x + dirx, xy.y + diry);
if (!check(graph, p) || random.nextFloat() < dirProbability) {
do {
setDir();
p = new Point(xy.x + dirx, xy.y + diry);
} while (!check(graph, p));
}
xy = p;
path.add(p);
setAlive(graph);
}
}
boolean check(int[][] graph, Point p) {
if (p.x < 0 || p.y < 0 || p.x >= graph.length || p.y >= graph.length) {
return false;
}
if (graph[p.y][p.x] == 1) {
return false;
}
return true;
}
@Override
public int hashCode() {
return Objects.hash(this.path.get(0), this.path.get(this.path.size() - 1));
}
@Override
public boolean equals(Object obj) {
Ant a2 = (Ant) obj;
return this.path.get(0).equals(a2.path.get(0))
&& this.path.get(this.path.size() - 1).equals(a2.path.get(a2.path.size() - 1));
}
}
Bei 10 Ameisen pro Punkt:
(1,1)->(1,2)->(1,3)->(1,4)->(1,5)->(0,5)->(0,6)
(0,6)->(0,5)->(0,4)->(0,3)->(0,2)->(0,1)->(0,0)->(1,0)->(2,0)->(3,0)->(4,0)->(5,0)->(6,0)->(6,1)->(6,2)->(6,3)->(6,4)->(5,4)->(4,4)
(4,4)->(3,4)->(2,4)->(1,4)->(0,4)->(1,4)->(2,4)->(3,4)->(4,4)->(5,4)->(6,4)->(6,5)->(6,6)->(6,5)->(6,4)->(6,3)->(6,2)->(6,1)->(6,0)->(5,0)->(4,0)->(3,0)->(2,0)->(1,0)->(0,0)->(1,0)->(2,0)->(3,0)->(4,0)->(5,0)->(6,0)->(6,1)->(5,1)->(4,1)->(3,1)
(3,1)->(4,1)->(5,1)->(6,1)->(6,0)->(5,0)->(4,0)->(3,0)->(2,0)->(1,0)->(0,0)->(1,0)->(2,0)->(3,0)->(4,0)->(5,0)->(6,0)->(5,0)->(4,0)->(3,0)->(2,0)->(1,0)->(0,0)->(1,0)->(2,0)->(1,0)->(0,0)->(1,0)->(1,1)
Bei 100 Ameisen pro Punkt:
(3,1)->(3,0)->(2,0)->(1,0)->(1,1)
(1,1)->(0,1)->(0,2)->(0,3)->(0,4)->(0,5)->(0,6)
(0,6)->(0,5)->(0,4)->(1,4)->(2,4)->(3,4)->(4,4)
(4,4)->(5,4)->(6,4)->(6,3)->(6,2)->(6,1)->(6,0)->(6,1)->(5,1)->(4,1)->(3,1)
Bei 1000 Ameisen pro Punkt:
(3,1)->(3,0)->(2,0)->(1,0)->(1,1)
(1,1)->(0,1)->(0,2)->(0,3)->(0,4)->(0,5)->(0,6)
(0,6)->(0,5)->(0,4)->(1,4)->(2,4)->(3,4)->(4,4)
(4,4)->(5,4)->(6,4)->(6,3)->(6,2)->(6,1)->(5,1)->(4,1)->(3,1)
Bei 10000 Ameisen pro Punkt:
(3,1)->(3,0)->(2,0)->(1,0)->(1,1)
(1,1)->(0,1)->(0,2)->(0,3)->(0,4)->(0,5)->(0,6)
(0,6)->(1,6)->(2,6)->(3,6)->(4,6)->(4,5)->(4,4)
(4,4)->(5,4)->(5,3)->(5,2)->(5,1)->(4,1)->(3,1)
Bei 10000 Ameisen pro Punkt wäre der Pfad also „optimal“. Hier auch nochmal als Grafik (grün = Laufwege):
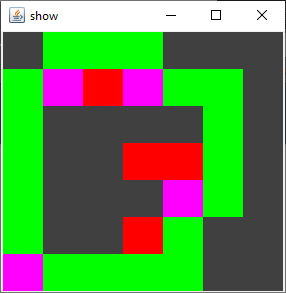
Warnung
@Adriano10 : Der Code, den CyborgBeta da postet, hat mit einem Ameisenalgorithmus (soweit ich das erfasse) nichts zu tun. (Nur weil da eine Klasse Ant drin vorkommt, heißt das nicht, dass das ein „Ameisenalgorithmus“ ist).
Natürlich könnte ich das mit einem Schulternzucken abtun, und sagen: „Schlechte Frage -> Schlechte Antwort“, aber ich wolllte darauf hinweisen.
Sowas wie https://www.baeldung.com/java-ant-colony-optimization leifert etwas Code. Natürlich ist das nicht direkt auf dein Problem übertragbar, weil du nicht direkt einen Graphen hast, sondern dieses Gitter, aber … über Details könnte man lange reden, wenn man sie (hier) als relevant ansehen würde.
Danke, Marco13, nächstes mal stelle ich komplette Aufgabestellung vor…
Ich dank euch, ich wurde euch schon zweites Mal sehr geholfen und wenn ich mich euch nicht aufdränge, lade ich die für mich unklare Dingen.
Danke euch noch mal
