Man kann sich da lange damit beschäftigen, auf unterschiedlichsten technischen Ebenen.
Auf der obersten Ebene ist das „irgendein Dimensionsreduktionsverfahren“ (etwas ungenau: eine Projektion). Das heißt man hat im einfachsten Fall nur das, was eben durch double[][] run(double input[][]) angeboten wird: Man schmeißt einen Array mit „hochdimensionalen“ Punkten rein (z.B. 100-dimensionale Punkte), und bekommt einen Array mit „niedrig(er)dimensionalen“ Punkten (meistens 2D-Punkte, weil man die schön darstellen kann).
Das gleiche gibt’s an sich auch mit PCA, MDS, oder anderen DimRed-Verfahren. Aber t-SNE hat vergleichsweise viel Aufmerksamkeit bekommen, weil es Ausgaben liefert, die in mancher Hinsicht „gut“ sind. Für „gut“ gibt es beliebig ausgefeilte Metriken, da wurden schon etliche Dissertationen drüber erarbeitet, aber stark vereinfacht gesagt: t-SNE bewirkt, dass Punkte, die im hochdimensionalen Raum „nah beieinander“ liegen, auch im niedrigdimensionalen Raum „nah beieinander“ liegen. (Das Verfahren ist in anderer Hinsicht „schlecht“, weil große Abstände nicht notwendigerweise groß bleiben, und es ist hochgradig nichtlinear, aber … das sind die Trade-Offs, die man da halt machen muss…)
Das ganze ist intern etwas stochastisch (dafür steht das S  ) und nicht-deterministisch. Aber am oben gezeigten Screenshot sieht man vielleicht schon, was das bedeutet: Die Eingaben sind 784-dimensionale Punkte - nämlich Bildchen von handschriftlichen Ziffern (oben rechts, bei der Maus, sieht man eine
) und nicht-deterministisch. Aber am oben gezeigten Screenshot sieht man vielleicht schon, was das bedeutet: Die Eingaben sind 784-dimensionale Punkte - nämlich Bildchen von handschriftlichen Ziffern (oben rechts, bei der Maus, sieht man eine 6). Und diese „Blobs“ die man da sieht sind die 2D-Ergebnisse, eingefärbt nach den Ziffern. Und man sieht, dass die Ziffern von 0 bis 9 recht klar abgegrenzte Grüppchen bilden (quasi „Cluster“ - nicht ganz der richtige Begriff, aber sinngemäß).
Wie das ganze genau intern funktioniert hatte ich mir nur vergleichsweise oberflächlich angesehen. Wie gesagt, da wird viel „random“ initialisiert, und dann läuft in vielen Iterationen etwas, was man sich im weitesten Sinne wie ein „Energieminimierungsverfahren“ oder eine Art „Simulated Annealing“ vorstellen kann: Wenn die Punkte in bezug auf ihre 2D-Neighbors (da haben wir das N) eine Einbettung (E) finden, in der sie sich „wohl“ fühlen, weil die nD-Abstände auch klein sind, ist das gut. Wenn nicht, versuchen sie eine Position zu finden, die besser zu den nD-Abständen passt.

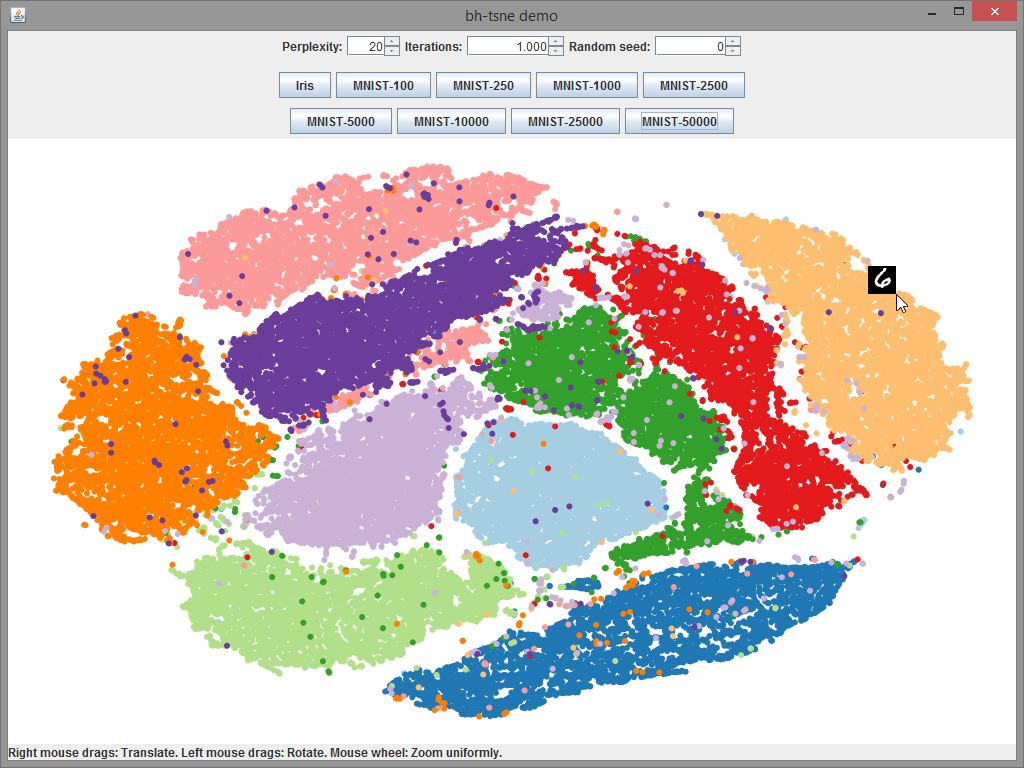
 ) und nicht-deterministisch. Aber am oben gezeigten Screenshot sieht man vielleicht schon, was das bedeutet: Die Eingaben sind 784-dimensionale Punkte - nämlich Bildchen von handschriftlichen Ziffern (oben rechts, bei der Maus, sieht man eine
) und nicht-deterministisch. Aber am oben gezeigten Screenshot sieht man vielleicht schon, was das bedeutet: Die Eingaben sind 784-dimensionale Punkte - nämlich Bildchen von handschriftlichen Ziffern (oben rechts, bei der Maus, sieht man eine 