Hier sind doch nicht nur Softis, sondern auch echte Mathematiker …
Hat sich schon mal jemand daran versucht, und wenn ja, zu welchem Ergebnis ist dieser gelangt?
Ich habe dafür einen wahrhaft wunderbaren Beweis gefunden. Aber leider sind die Formatierungsmöglichkeiten für mathematische Formeln hier im Forum zu eingeschränkt, um ihn zu posten.
1 „Gefällt mir“
Dann mal anders gefragt … der „Beweisbaum“ auf der rechten Seite auf der Seite von Spektrum sieht doch schon vielversprechend aus … Wieso genügt dieser nicht?
Zu oft zu unterschiedliches Verhalten?
Ja, genau wie es bei Riemann laufen wird:
(EDIT: Die Quelle is http://abstrusegoose.com/210 - leider scheint die Seite inzwischen tot zu sein. Ein echter Verlust 
)
1 „Gefällt mir“
@Marco13 Was passiert, wenn 2100 ad ChatGPT die Riemann beweist/löst?
Ein neuer Ansatz zur Lösung der Collatz-Vermutung.
In seinem Beitrag „Das Collatz-Problem“ auf „www.Spektrum.de“ formuliert Herr G. J. Wirsching sieben Fragen, die bei der Lösung des Problems helfen könnten.
1. Gibt es noch andere Zykel? Wieviele, und welche?
2. Endet jede f3-Trajektorie in einem Zykel, oder gibt es eine divergente Trajektorie?
3. Von welchen Zahlen kann man beweisen, daß sie die 3n + 1 Vermutung erfüllen?
4. Was passiert, wenn man 3n + 1 durch qn + 1 ersetzt?
5. Gibt es noch andere interessante Verallgemeinerungen?
6. Kann es sein, daß das Collatz-Problem nicht entscheidbar ist?
7. Gibt es interessante Erweiterungen oder Umformulierungen des Collatz-Problems?
(Das Collatz-Problem - Lexikon der Mathematik)
Ich habe hinsichtlich der Fragen 4,5 und 7 einen neuen Ansatz gefunden.
Grundlage ist die Überlegung, dass sich das Problem allgemeiner darstellen ließe, wenn man zugrunde legt, dass es sich bei 2 und 3 um Primzahlen handelt.
Die Collatz-Funktion basiert dann nicht auf gerade und ungerade Zahlen, sondern auf Primzahlen.
Die Collatz-Funktion lautet wie folgt:
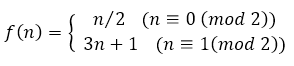
(Leider kann ich als Neumitglied hier nicht wirklich arbeiten und muss meinene Beitrag stückeln.)
und sie würde als allgemeine Funktion wie folgt lauten:
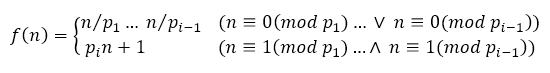
Für p_i gilt: p_i ist Element der Primzahlen und p_1… p_(i-1) umfasst alle Primzahlen < p_i
(_i steht für den Index (i))
Die vierte Frage von Herrn Wirsching, was geschieht, wenn qn + 1, wäre dann (für q =5)wie folgt zu beantworten.
4.Ergebnisse
Hier einige Ergebnisse:
| Funktion | Getestet bis | Konvergiert gegen |
|---|---|---|
| B5 | 4.000.000 | 1 |
| B7 | 3.000.000 | 1 |
| B11 | 100.000 | 1, 17 |
| B13 | 100.000 | 1 , 19 |
| B17 | 500.000 | 1,43 |
| B19 | 100.000 | 1,46063 |
| B23 | 100.000 | 1,179 |
| B29 | 100.000 | 1 |
| B31 | 100.000 | 1, 67 |
| B37 | 100.000 | 1, 2173 |
| B41 | 100.000 | 1 |
| B43 | 400.000 | 1,208513 |
| B47 | 400.000 | 1,2243 |
| B53 | 400.000 | 1,19559 |
| B59 | 400.000 | 1,73 |
| B61 | 400.000 | 1,97,199,26833 |
| B67 | 400.000 | 1,181 |
| B71 | 400.000 | 1,306511 |
| B73 | 400.000 | 1,14929,140729 |
| B79 | 1.500.000 | 1 |
| B83 | 400.000 | 1,89,4049 |
| B89 | 1.000.000 | 1 |
| B97 | 400.000 | 1,1109 |
| B101 | 500.000 | 1,661 |
| B103 | 1.000.000 | 1,11131 |
| B107 | 1.000.000 | 1 |
| B109 | 1.000.000 | 1 |
| B113 | 1.000.000 | 1,1181 |
| B127 | 1.000.000 | 1 |
| B131 | 500.000 | 1 |
| B137 | 500.000 | 1 |
| B139 | 500.000 | 1 |
| B149 | 500.000 | 1 |
| B151 | 500.000 | 1,20173 |
| B157 | 700.000 | 1 |
| B163 | 700.000 | 1,383 |
| B167 | 700.000 | 1,1871,2027 |
| B173 | 700.000 | 1,2113 |
| B179 | 700.000 | 1 |
| B181 | 700.000 | 1,991 |
| B191 | 700.000 | 1 |
| B997 | 400.000 | 1 |
| B1009 | 700.000 | 1 |
(in der letzten Spalte sind die unterschiedlichen Endpunkte mit Komma getrennt.
zb. B11 Startwert: 17 die Folge endet auf 17:
17,188,94,47,518,259,37,408,204,102,51,17,
zb. B13 Startwert: 19 die Folge endet auf 19:
19,248,124,62,31,404,202,101,1314,657,219,73,950,475,95,19,)
Funktion B19
.
3. Eine Beispielberechnung mit B5
Der Startwert (n) = 23 ist weder durch 3 noch durch 2 teillbar also:
5 * 23 +1 = 116
Der neue Startwert 116 ist durch 2 teilbar:
116/2 = 58 >> durch 2 teilbar
58/2= 29
Zahlenfolge bis hier
23,116,58,29
weitere Schritte
5 * 29 +1 = 146
46/ 2 = 73
5 * 73 +1 = 366
366 /2=183
183/3=61
5*61+1=306
306/2=183
153/3=51
51/3=17
… usw
hier die Folge der Funktion B5 mit dem Startwert 23: 23,116,58,29,146,73,366,183,61,306,153,51,17,86,43,216,108,54,27,9,3,1,6,
Wenn diese Regeln ähnliche Resultate liefern wie die Collatz-Funktion, dann könnte dieser Ansatz bei der Beantwortung der ersten 2 Fragen des Herrn Wirsching helfen. Immerhin hätten die „Mathematik“ damit unendlich viele Collatz Varianten.
Ich habe das mit meinen schmalen Mitteln getestet und muss anmerken, dass meine Überlegung stichhaltig ist.
Im unteren Zahlenbereich, als so bis 4.000.000 habe ich testweise mit diversen Primzahlen gearbeitet und frappante Ähnlichkeiten mit der Collatz Funktion feststellen können.
2.
Diese Verallgemeinerung der Collatz-Funktion habe ich die Binder-Verallgemeinerung genannt. Um die Funktionen auseinanderzuhalten, nutze ich im Folgenden das B + die Primzahl p_i, die für q in qn + 1 (Frage 4 oben) eingesetzt wird.
B5 meint also
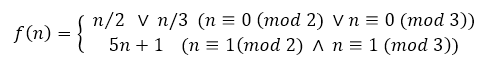
Für p_i=7 ergibt sich dann die Funktion
- 7 ist Element von (ℙ)
- 2, 3, 5 <7 und Elemente von (ℙ) und n/2, n/3, n/5 sind zu befolgen
- Das Ergebnis dient als neuer Startwert.
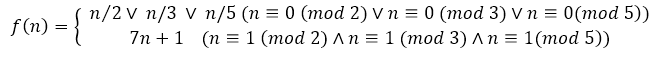
Und so weiter.
Für p_i=5 ergibt sich die Funktion (B5):
- 5 ist Element von (ℙ)
- 2< 5, 3 <5 und 2,3 sind Elemente von (ℙ)
- Das Ergebnis dient als neuer Startwert.
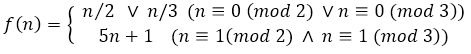
Jetzt fehlt das Ganze ja eigentlich nur noch für gerade und ungerade Zahlen