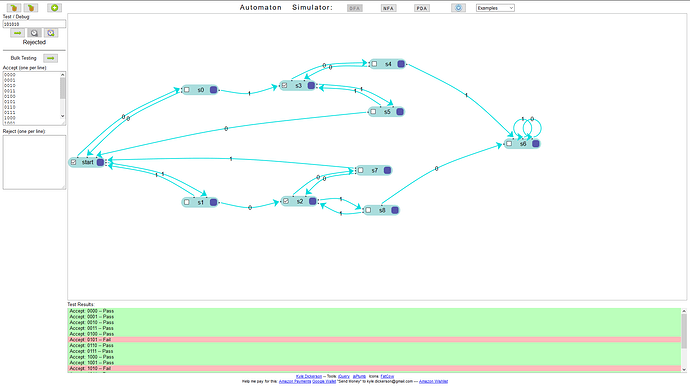
Quelle: http://automatonsimulator.com/
Spielstand (damit ihr euch nicht Mühe geben müsst):
{"type":"DFA","dfa":{"transitions":{"start":{"0":"s0","1":"s1"},"s0":{"0":"start","1":"s3"},"s1":{"0":"s2","1":"start"},"s3":{"0":"s4","1":"s5"},"s4":{"0":"s3","1":"s6"},"s5":{"0":"start","1":"s3"},"s2":{"0":"s7","1":"s8"},"s7":{"0":"s2","1":"start"},"s8":{"0":"s6","1":"s2"},"s6":{"0":"s6","1":"s6"}},"startState":"start","acceptStates":["start","s3","s2"]},"states":{"start":{"isAccept":true},"s0":{"top":197,"left":315},"s1":{"top":510.0000305175781,"left":315},"s3":{"isAccept":true,"top":185,"left":587},"s2":{"isAccept":true,"top":507.0000305175781,"left":591},"s4":{"top":125,"left":837},"s5":{"top":258,"left":834},"s6":{"top":347,"left":1212},"s7":{"top":421,"left":799},"s8":{"top":532.0000305175781,"left":820}},"transitions":[{"stateA":"start","label":"0","stateB":"s0"},{"stateA":"start","label":"1","stateB":"s1"},{"stateA":"s0","label":"0","stateB":"start"},{"stateA":"s0","label":"1","stateB":"s3"},{"stateA":"s1","label":"0","stateB":"s2"},{"stateA":"s1","label":"1","stateB":"start"},{"stateA":"s3","label":"0","stateB":"s4"},{"stateA":"s3","label":"1","stateB":"s5"},{"stateA":"s4","label":"0","stateB":"s3"},{"stateA":"s4","label":"1","stateB":"s6"},{"stateA":"s5","label":"0","stateB":"start"},{"stateA":"s5","label":"1","stateB":"s3"},{"stateA":"s2","label":"0","stateB":"s7"},{"stateA":"s2","label":"1","stateB":"s8"},{"stateA":"s7","label":"0","stateB":"s2"},{"stateA":"s7","label":"1","stateB":"start"},{"stateA":"s8","label":"0","stateB":"s6"},{"stateA":"s8","label":"1","stateB":"s2"},{"stateA":"s6","label":"0","stateB":"s6"},{"stateA":"s6","label":"1","stateB":"s6"}],"bulkTests":{"accept":"0000\n0001\n0010\n0011\n0100\n0110\n0111\n1000\n1001\n1011\n1100\n1101\n1111","reject":"0101\n1010\n101010"}}
Fragen an @bisaflor :
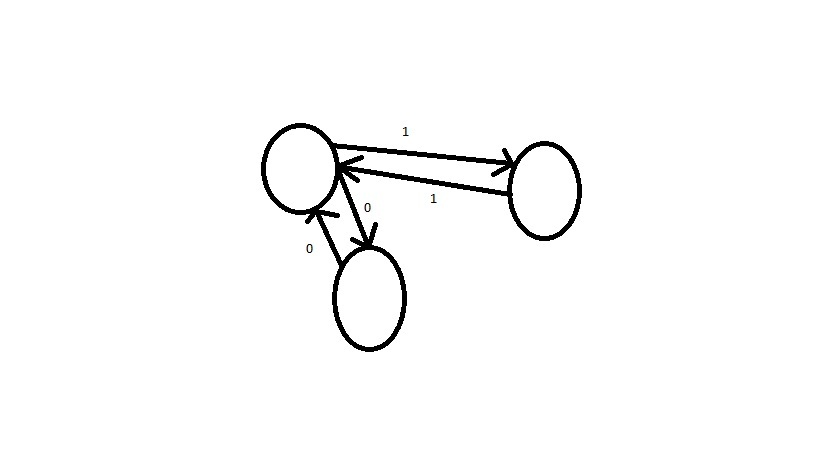
- Was bedeuten die Zustände s3 und s2?
- Was bedeutet der Zustand start?
- s6 ist der verbrannte Zustand.
Hint:
Bei Bulk Testing schreibt man das nicht zu Akzeptierende nicht zu Accept.  (Hab ich wohl verstanden)
(Hab ich wohl verstanden)

 (Hab ich wohl verstanden)
(Hab ich wohl verstanden)