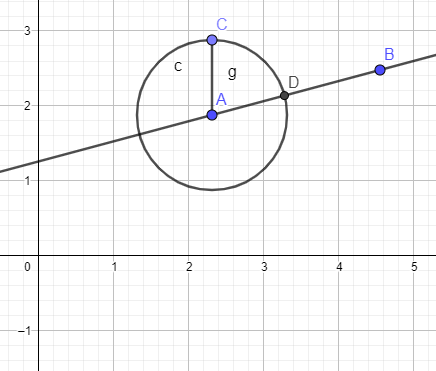
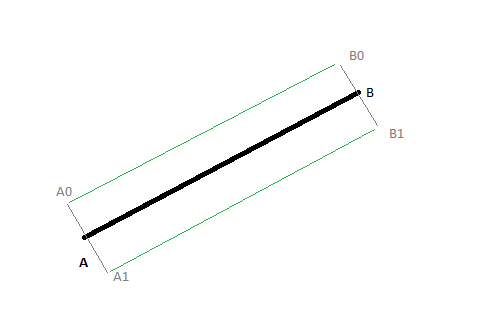
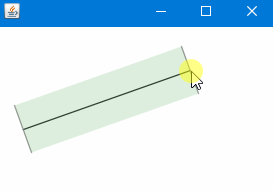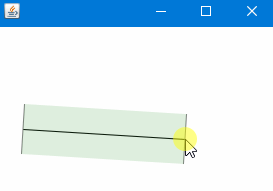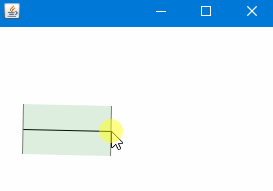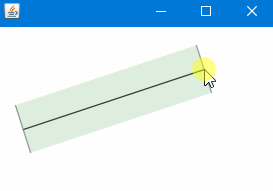
Tada! Besser?:
private void darawLine(Graphics2D g2d, Point a, Point b, int thickness) {
Point2D.Double c = new Point2D.Double(-(b.y - a.y), (b.x - a.x));
double len = Math.sqrt(c.x * c.x + c.y * c.y);
c.x /= len;
c.y /= len;
Point a0 = new Point((int) (a.x + c.x * thickness), (int) (a.y + c.y * thickness));
// g2d.drawString("0", a0.x, a0.y);
Point a1 = new Point((int) (b.x + c.x * thickness), (int) (b.y + c.y * thickness));
// g2d.drawString("1", a1.x, a1.y);
Point a2 = new Point((int) (b.x + c.x * -thickness), (int) (b.y + c.y * -thickness));
// g2d.drawString("2", a2.x, a2.y);
Point a3 = new Point((int) (a.x + c.x * -thickness), (int) (a.y + c.y * -thickness));
// g2d.drawString("3", a3.x, a3.y);
g2d.fillPolygon(new int[] { a0.x, a1.x, a2.x, a3.x }, new int[] { a0.y, a1.y, a2.y, a3.y }, 4);
}
Und hier wäre die eine komplette Anwendung dazu:
import java.awt.BasicStroke;
import java.awt.Canvas;
import java.awt.Graphics;
import java.awt.Graphics2D;
import java.awt.Point;
import java.awt.geom.Line2D;
import java.awt.geom.Point2D;
import java.util.Calendar;
import java.util.GregorianCalendar;
import java.util.Timer;
import java.util.TimerTask;
import javax.swing.JFrame;
import javax.swing.SwingUtilities;
public class Uhr extends JFrame {
private static final long serialVersionUID = 1L;
private Canvas canvas = new Canvas() {
private static final long serialVersionUID = 1L;
private void darawLine(Graphics2D g2d, Point a, Point b, int thickness) {
Point2D.Double c = new Point2D.Double(-(b.y - a.y), (b.x - a.x));
double len = Math.sqrt(c.x * c.x + c.y * c.y);
c.x /= len;
c.y /= len;
Point a0 = new Point((int) (a.x + c.x * thickness), (int) (a.y + c.y * thickness));
// g2d.drawString("0", a0.x, a0.y);
Point a1 = new Point((int) (b.x + c.x * thickness), (int) (b.y + c.y * thickness));
// g2d.drawString("1", a1.x, a1.y);
Point a2 = new Point((int) (b.x + c.x * -thickness), (int) (b.y + c.y * -thickness));
// g2d.drawString("2", a2.x, a2.y);
Point a3 = new Point((int) (a.x + c.x * -thickness), (int) (a.y + c.y * -thickness));
// g2d.drawString("3", a3.x, a3.y);
g2d.fillPolygon(new int[] { a0.x, a1.x, a2.x, a3.x }, new int[] { a0.y, a1.y, a2.y, a3.y }, 4);
}
@Override
public void paint(Graphics g) {
Graphics2D g2d = (Graphics2D) g;
int w = this.getWidth();
int h = this.getHeight();
int wh = Math.min(w, h);
int wh2 = wh / 2;
g2d.drawOval(5, 5, wh - 10, wh - 10);
for (int i = 0; i < 12; i++) {
int x0 = (int) (wh2 + (wh2 - 20) * Math.cos(Math.toRadians(360 / 12 * i)));
int y0 = (int) (wh2 + (wh2 - 20) * Math.sin(Math.toRadians(360 / 12 * i)));
int x1 = (int) (wh2 + (wh2 - 10) * Math.cos(Math.toRadians(360 / 12 * i)));
int y1 = (int) (wh2 + (wh2 - 10) * Math.sin(Math.toRadians(360 / 12 * i)));
darawLine(g2d, new Point(x0, y0), new Point(x1, y1), 5);
}
{
// Calibrate
Calendar calendar = GregorianCalendar.getInstance();
float minute = calendar.get(Calendar.MINUTE);
float hour = calendar.get(Calendar.HOUR) + (minute / 60f); // The hour pointer should tick every minute.
minute += calendar.get(Calendar.SECOND) / 60f; // The minute pointer should tick every second.
// Draw, wh2 is the center
int x0 = (int) (wh2 + (wh2 - 20) * Math.cos(Math.toRadians(360 / 60 * minute - 90)));
int y0 = (int) (wh2 + (wh2 - 20) * Math.sin(Math.toRadians(360 / 60 * minute - 90)));
int x1 = (int) (wh2 + (wh2 - 40) * Math.cos(Math.toRadians(360 / 12 * hour - 90)));
int y1 = (int) (wh2 + (wh2 - 40) * Math.sin(Math.toRadians(360 / 12 * hour - 90)));
darawLine(g2d, new Point(wh2, wh2), new Point(x0, y0), 5);
darawLine(g2d, new Point(wh2, wh2), new Point(x1, y1), 10);
}
}
};
public Uhr() {
add(canvas);
setSize(400, 400);
setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);
setVisible(true);
// Repaint every second.
new Timer().schedule(new TimerTask() {
@Override
public void run() {
SwingUtilities.invokeLater(new Runnable() {
@Override
public void run() {
canvas.repaint();
}
});
}
}, 1000, 1000);
}
public static void main(String[] args) {
new Uhr();
}
}
(Flackert die Analoguhr bei euch auch manchmal? )