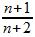Guten Tag,
ich soll mit vollständiger Induktion
zeigen.
Die Behauptung lautet:
also
Nach meiner Umformung komme ich auf
Was scheinbar auch richtig ist, denn:
Leider weiß ich nicht, welche Schritte notwendig sind, um mein Ergebnis ((n+1)/(n+2)) so umzuformen, dass ich als Ergebnis die Behauptungsgleichung bekomme. Kann mir das jemand bitte eklären?
Geht es um diese Aussage?
Entweder Polynomdivision oder du schreibst den Zähler ein bisschen um, indem du eine Null addierst.
n+1 = n+1+1-1 = n+2-1
Reicht dir das schon?
Danke für deine Antwort. Aber das suche ich leider nicht.
Ich möchte gerne wissen, wie ich
so umformen kann, dass
herauskommt.
[QUOTE=Quantum]Danke für deine Antwort. Aber das suche ich leider nicht.
Ich möchte gerne wissen, wie ich
so umformen kann, dass
herauskommt.[/QUOTE]
Die Antwort wurde dir gegeben 
Dann nochmal:
Ich sollte genauer hinschauen.
Vielen Dank euch beiden!
Da hat Eagle sich die Mühe gemacht, das TeX Paket zum laufen zu bekommen, und niemand nutzt es. So versteht das Board auch LaTeX:
[noparse][tex]\forall n\in \mathbb{N}: \sum\limits_{k=1}^n\frac{1}{k\left( k+1 \right)}[/tex][/noparse]
Das sieht dann so aus:
[tex]\forall n\in \mathbb{N}: \sum\limits_{k=1}^n\frac{1}{k\left( k+1 \right)}[/tex]