Tiwanaku

[Apo]

Hi,

ich arbeite gerade an einem Spiel basierend auf der Idee des Brettspiels Tiwanaku auf BGG.

Ich habe mich aber auf die Erstellung und das Lösen der Level im Sudokustil konzentriert und keine 1 zu 1 Umsetzung des Brettspiels gemacht. Hintergrund ursprünglich war, dass ich unenedlich Szenrien zum Spielen bekomme.

Regeln:
Wie bei Sudoku muss eine Matrix mit Zahlen gefüllt werden. Es gibt nur zwei Regeln:

• Jede Zahl darf ich jedem Bereich nur einmal vorkommen. Das bedeutet in einem „Waldbereich“, welcher 5 Felder groß ist, müssen die Zahlen von 1 bis 5. In einem Wasserbereich, welcher 3 Felder groß ist, kommen die Zahlen 1 bis 3 vor.
• Im direkten Umkreis darf eine Zahl nur 1 mal vorkommen (das bedeutet wenn eine 2 in der Mitte steht, darf keine 2 in der direkten 8 Nachbarschaft (links, links oben, oben, rechts oben, rechts, rechts unten, unten, links unten) sein.

Das Spiel ist jetzt schon komplett spielbar und macht (in meinen Augen) auch schon viel Spaß, gerade um kurze Wartezeiten zu überbrücken.
Spielbar ist es unter: Tiwanaku

Frage zur Erstellung der Level:
Ich hatte hier im Forum ja gefragt, wie ich ein Level am besten lösen kann, siehe Knuth's Algorithm X Frage - #17 von Apo und bin mit der Lösung auch sehr zufrieden. Aber nun habe ich noch Performanceprobleme bei der Erstellung eines Levels.
Aktuell gehe ich so vor, dass ich zuerst den Untergrund mit den Biomen erstelle und dann schaue, ob es dafür eine Lösung gibt.
Für kleinere Level klappt das auch in annehmbarer Geschwindigkeit, aber z.B. bei einem 9x9 Level geht die Erstellung des Untergrundes schnell, aber gefühlt 99% der Level haben keine Lösung und er versucht es wieder. Ich weiß, das bedeutet ich muss mehr Regeln bei der Erstellung der Biome implementieren, aber aktuell überlege ich, ob das überhaupt der Weg ist, den ich gehen sollte oder ob nicht vielleicht ein komplett neuer Ansatz gut wäre. Also vielleicht zuerst mit Zahlen füllen (nach den Regeln und dann schauen, ob daraus ein Untergrund werden kann) oder ein anderer Ansatz. Habt ihr da eine Idee? Wie würdet ihr vorgehen?

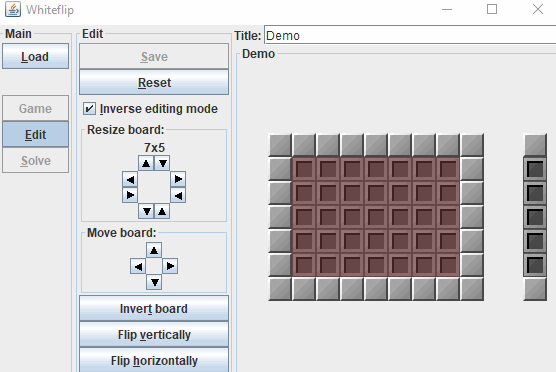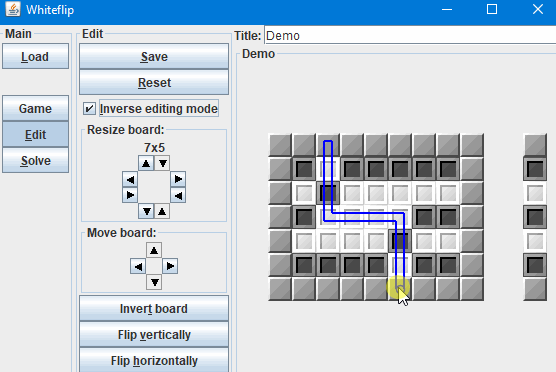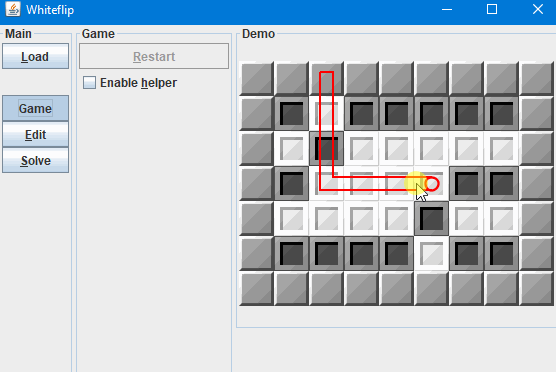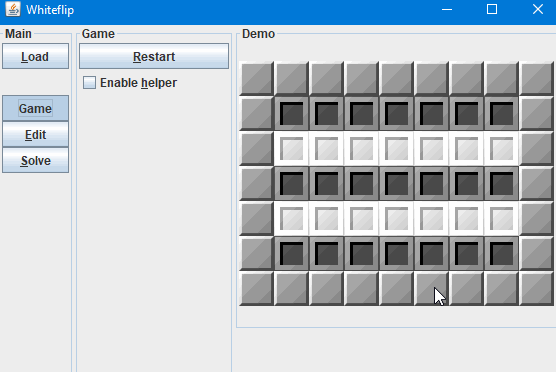
Screenshot:

[Marco13]

Die genaue Reihenfolge beim Erstellen ist mir nicht klar, oder wo dort welche Form von Zufall eine Rolle spielt. Wie werden denn z.B. die initialen (roten) Zahlen festgelegt? Wer legt fest (und wie), dass nicht „alles Wald“ ist? (Schon dass Biome nicht zusammenhängend sind hat mich etwas überrascht, aber ist nicht direkt relevant für die Lösung)

Ich könnte mir vorstellen, dass man beim Erstellen eine ähnliche Strategie verwenden könnte, wie beim Lösen - in dem Sinne, dass man immer mehr Biome festlegt, und wenn man merkt, dass es damit „unmöglich“ wird, macht man einen Schritt zurück.

---

Ich hatte ja schon erwähnt, dass ich denke, dass man das Problem an sich (als nicht die Erstellung, sondern die Lösung) auch als CSP modellieren könnte. Ich hab’ da mal schnell was hingehackt, aber das ist noch nicht richtig (z.B. nimmt es „zusammenhängende“ Biome an, aber das wäre leicht zu ändern).

Das ganze benutzt nur https://mvnrepository.com/artifact/com.googlecode.aima-java/aima-core/3.0.0 als dependency, und ich dumpe es einfach mal hier

import aima.core.search.csp.Assignment;
import aima.core.search.csp.CSP;
import aima.core.search.csp.CSPStateListener;
import aima.core.search.csp.ImprovedBacktrackingStrategy;
import aima.core.search.csp.SolutionStrategy;

public class TiwanakuCSPTest
{
    public static void main(String[] args)
    {
        int F = 0;
        int W = 1;
        int S = 2;
        int field[][] = new int[][]{
            {F, W, W }, 
            {F, F, W }, 
            {S, F, F} 
        };
        int array[][] = new int[][]{
            {5, 0, 2 }, 
            {0, 0, 0 }, 
            {0, 0, 0 } 
        };
        
        CSP csp = new TiwanakuCSP(field, array);
        StepCounter stepCounter = new StepCounter();
        SolutionStrategy solver;
        solver = new ImprovedBacktrackingStrategy(true, true, true, true);
        solver.addCSPStateListener(stepCounter);
        stepCounter.reset();
        
        System.out.println(solver.solve(csp.copyDomains()));
        System.out.println(stepCounter.getResults() + "\n");
    }
    
    protected static class StepCounter implements CSPStateListener
    {
        private int assignmentCount = 0;
        private int domainCount = 0;
        

        @Override
        public void stateChanged(Assignment assignment, CSP csp)
        {
            ++assignmentCount;
        }

        @Override
        public void stateChanged(CSP csp)
        {
            ++domainCount;
        }

        public void reset()
        {
            assignmentCount = 0;
            domainCount = 0;
        }

        public String getResults()
        {
            StringBuffer result = new StringBuffer();
            result.append("assignment changes: " + assignmentCount);
            if (domainCount != 0)
                result.append(", domain changes: " + domainCount);
            return result.toString();
        }
    }
}

import java.util.ArrayList;
import java.util.LinkedHashMap;
import java.util.List;
import java.util.Map;

import aima.core.search.csp.CSP;
import aima.core.search.csp.Domain;
import aima.core.search.csp.Variable;
import aima.core.search.csp.examples.NotEqualConstraint;

public class TiwanakuCSP extends CSP
{
    public TiwanakuCSP(int field[][], int array[][])
    {
        int rows = field.length;
        int cols = field[0].length;
        for (int r = 0; r < rows; r++)
        {
            for (int c = 0; c < cols; c++)
            {
                addVariable(new Variable("F" + r + c));
            }
        }

        Map<Integer, List<Variable>> fieldVaribles =
            new LinkedHashMap<Integer, List<Variable>>();
        for (int r = 0; r < rows; r++)
        {
            for (int c = 0; c < cols; c++)
            {
                int f = field[r][c];
                List<Variable> list = fieldVaribles.computeIfAbsent(f,
                    i -> new ArrayList<Variable>());
                list.add(new Variable("F" + r + c));
            }
        }

        for (int r = 0; r < rows; r++)
        {
            for (int c = 0; c < cols; c++)
            {
                Variable v = new Variable("F" + r + c);
                if (array[r][c] != 0)
                {
                    setDomain(v, new Domain(new Integer[]
                    { array[r][c] }));
                }
                else
                {
                    int f = field[r][c];
                    List<Variable> x = fieldVaribles.get(f);
                    List<Integer> vs = new ArrayList<Integer>();
                    for (int i = 0; i < x.size(); i++)
                    {
                        vs.add(i + 1);
                    }
                    Domain values = new Domain(vs);
                    setDomain(v, values);
                }
            }
        }
        for (int r = 0; r < rows; r++)
        {
            for (int c = 0; c < cols; c++)
            {
                for (int dr = -1; dr <= 1; dr++)
                {
                    for (int dc = -1; dc <= 1; dc++)
                    {
                        if (dr == 0 && dc == 0)
                        {
                            continue;
                        }
                        int nr = r + dr;
                        int nc = c + dc;
                        if (nr >= 0 && nr < rows && nc >= 0 && nc < cols)
                        {
                            Variable v = new Variable("F" + r + c);
                            Variable n = new Variable("F" + nr + nc);
                            addConstraint(new NotEqualConstraint(v, n));
                        }
                    }
                }
            }
        }

        for (Integer key : fieldVaribles.keySet())
        {
            List<Variable> variables = fieldVaribles.get(key);
            for (int i = 0; i < variables.size(); i++)
            {
                for (int j = i + 1; j < variables.size(); j++)
                {
                    Variable vi = variables.get(i);
                    Variable vj = variables.get(j);
                    addConstraint(new NotEqualConstraint(vi, vj));
                }
            }
        }
    }
}

Vielleicht schau’ ich bei Gelegenheit nochmal genauer, wie man das „richtig“ machen könnte (und vielleicht könnte man mit sowas auch das Erstellen modellieren, modulo der Frage nach dem Zufall…)

[Apo]

Hallo Marco,

aktuell gehe ich wie folgt vor:

Ich erstelle mir den Untergrund komplett zufällig. Dazu gebe ich an wie viele 5 Biome ich haben möchte und wie viele 4er Biome und dann versuche ich nacheinander erst die 5 Biome zufällig zu platzieren und dann die vierer zufällig. Wenn ich es 100 mal nicht hinbekomme ,dann breche ich ab und versuche es mit verschiedenen anderen offenen Stellen zu füllen (3er und 2 und 1er Stellen halt).

Wenn der Untergrund erstellt wurde, teste ich mit Knuths Algorithm X, ob es mindestens eine Lösung gibt.
Falls ja, hole ich mir alle Lösungen, wähle zufällig eine aus und lösche immer mehr Zahlen. Nach jedem Zahlenlöschen aus der Lösung, teste ich ob es noch eineindeutig ist. Falls ja, lösche ich weiter. Bei EASY z.B. lösche ich 70% der Zahlen. Die übrig gebliebenen werden dann rot umrandet und sind fest.

Was ich gerne testen will nun, wenn ich Zeit finde:
Bei der Erstellung des Untergrundes, also Platzierung eines 5er bioms, es gleich mit Zahlen füllen und testen, ob es überhaupt noch eine valide Lösung geben kann und erst dann weiter gehen mit dem Setzen eines neuen Bioms bis es fertig ist.

[Crian]

Auch wenn ich gerade inhaltlich nichts dazu beitragen kann, ich finde die Spielidee sehr schick. Wird das dann auch wieder ein Handyspiel? Dein Hitori spiele ich da nach wie vor sehr gern, um Wartezeiten zu überbrücken.

[Apo]

Ja, ich spiele es auch jetzt schon hauptsächlich auf dem Smartphone. (ist auch performanter als die WebLösung) und das macht mehr Spaß als viele andere Spiele von mir. Gerade in Bus und Bahn, am Abend kurz vor dem Schlafen und beim Arzt (ja, ich werde alt) passt es super, da es so schnell geht. =)

Aber ich wollte es erst in den PlayStore bringen, wenn ich es richtig performant bis zu 9x9 hinbekomme. Aktuell geht es (auf meinem OnePlus7t) nur bis 7x5 schnell. Und das geht gegen meine „Entwicklerehre“ so etwas offiziell rauszubringen. Deshalb auch dieser Thread und die Fragen.

[Marco13]

@Apo

da es so schnell geht.

Ich hatte zwei, drei mal versucht, eins von den „einfachen“ zu lösen, aber dann aufgegeben. Mir fehlt da die Geduld.

@Apo

Wenn ich es 100 mal nicht hinbekomme…

Einerseits kann es legitim sein, so eine Art „Greedy-Strategie“ zu verwenden: „Versuche, fünf 5er-Biome zu erstellen, und wenn’s nicht klappt, gib’ dich mit 4er-Biomen zufrieden“. Aber es wirkt immer etwas… hilflos und un-deterministisch.

Ich hatte grob überlegt, wie ein Ansatz dafür aussehen könnte. (Und eben gerade vieeel mehr Zeit mit dem Erstellen einer Klasse namens TiwanakuGen verbracht, als ich sollte…). Ein Gedanke, ganz grob:

• Starte mit dem leeren Feld
• Wirf ein paar „seeds“ für „Biom-Gebiete“ in das Feld - bestehend aus (biom,zahl) an Positionen (x,y)
• Mach eine Art „Breitensuche“:
  • Für jedes Biom-Gebiet: Betrachte alle angrenzenden Felder (also Felder, durch die das Biom-Gebiet vergrößert werden könnte)
    • Vergrößere das Gebiet mit diesem Feld
    • Ist das Spielbrett damit voll und konsistent belegt?
      • Ja: Profit!
      • Nein: Nimm das letzte Feld wieder weg, und versuche ein anderes

Das ist natürlich ein Backtracking, und … das hat immer das Potential exponentieller Laufzeit. Man muss ggf. sehr geschickt sein, um möglichst früh zu prunen. Z.B. dass er hier…

At 3 0 there is B 3, with 1 flood filled fields
D2 __ A2 B3 C2 C3
D5 E4 E5 D1 E4 E5
D3 __ C2 D3 __ D3
D4 E5 E4 D5 E4 E5

erkennt, dass „B3“ in der ersten Zeile keinen Sinn ergibt, weil es kein B1 und B2 mehr geben kann. Aber ich glaube, in meinem aktuellen Ansatz ist eine Sache haarsträubend schlecht gelöst, nämlich allgemein die Handhabung der Zahlen, die vorgegeben sein können. Er setzt dort eben die B3 hin (nachdem er auch B1 und B2 dort hingesetzt hat), aber vielleicht sollte er das nicht. Es könnte sein, dass es viel geschickter wäre, z.B. zufällige zusammenhängende Bereiche zu füllen, und dann Zahlen (systematisch!) durchzuprobieren. Aber das ist nur händewedeln - an irgendeinem Punkt veschwimmt die Grenze zwischen „dem systematischen Erstellen einer konsistenten Lösung“ und „dem Erstellen eines Solvers“.

---

Kleiner (halb?) off-topic Ausflug:

Es gab mal ein cooles Spiel online, das nannte sich „Blackflip“ (stark angelehnt an Polarium - Wikipedia ). Dort konnten Leute „Boards“ erstellen und hochladen, und man konnte die spielen, es wurde angezeigt, wie viele Leute ein Board schon gelöst (oder aufgegeben) hatte, und man hat dann solche grünen Marker/Flags bekommen für die, die man schon gelöst hatte und so…

Das Spielprinzip war dort:

• Es gibt ein Board mit schwarzen und weißen Feldern
• Man muss einen einzelnen, zusammenhängenden Pfad durch das Board malen, bei dem man jedes Feld höchstens einmal besucht (mit einem „Rand“ aus Hilfsfeldern)
• Wenn der Pfad fertig war, wurde jedes (anfangs) weiße Feld schwarz, und jedes schwarze Feld weiß
• Im daraus entstehenden Board muss jede Zeile die gleiche Farbe haben

Und … einige der Boards sahen einfach aus, und ich bin (wie viele andere) gnadenlos und frustrierenderweise daran gescheitert. Deswegen habe ich dann einen Solver geschrieben … und… weil’s cool war, auch gleich noch einen Editor dazu.

Auch da stellt sich die Frage: Kann man so ein Board überhaupt lösen, wenn man einfach rumklickt und schwarze/weiße Felder setzt?

Und um sicherzustellen, dass es eine Lösung für die Boards gibt, die man erstellt, habe ich dann einen „Inverse editing mode“ angeboten: Man erstellt nicht das Board, sondern malt den Lösungspfad - und daraus wird das Board erstellt, was mit diesem Pfad eine Lösung ergibt.

Eine kleines demo-GIF (wo man im ‚Game‘ Modus dann auch das Spiel selbst sieht):

(Ja, das Spiel hieß „Blackflip“, und meine Version dann halt „Whiteflip“ )

---

Der Grundgedanke, übertragen auf Tiwanaku, wäre: Kann man nicht gezielt und systematisch DIE Lösung erstellen, ohne da „100 mal“ zu probieren, und 100 mal den Solver anwerfen zu müssen…?

[Apo]

Danke Marco für dein ausführliches Feedback.

zu 1.) Vielleicht hilft es dir die Hilfe Funktion oben rechts auszuprobieren, da sieht man aufgrund der 2 Regeln welche Möglichkeiten es gerade noch gibt. Zum Lösen wenn man mal hängt super, ansonsten immer aus machen.

zu 2.) Ja, genau wie du beschrieben hast, würde ich gerne vorgehen nun, bloß dass ich wirklich komplett ein Biom fertig stelle und mit zahlen fülle, dann das nächste, falls es nicht mehr geht dann wieder Backtracking … trotzdem wie du schreibst problematisch das exponentieller Aufwand. Bin gespannt wie es sich ausgeht, meine nächste Zeit ist nur leider etwas voll und ich werde es wieder richtig in 2 Wochen dazu kommen es zu erstellen und auszuprobieren. Aber ich muss es lösen =)

zu 3.)
Polarium habe ich damals auch nachgemacht.

Wunderbares Spiel. =)

Und ja die aktuelle Lösung verwerfe ich auch nicht für Tiwanaku, sondern versuche x weitere Möglichkeiten zur Erstellung der Levels zu erschaffen und dann eine sehr gute zu finden. =)

siehe

[Marco13]

Die „Hilfe“ hatte ich gesehen, und dann auch versucht, mich daran entlang zu hangeln, aber … ich bin eher jemand, der 100 Stunden in einen Solver steckt, als 10x1 Stunde in die manuelle Lösung

Das praktische, wenn man nicht nur das Spiel sondern einen Solver schreibt, ist, dass solche „Hilfen“ aus den Solvern oft automatisch rausfallen. Genau das sind ja die Pruning/Backtracking-Kriterien:

(Das war übrigens das Board, das mich zum Erstellen des Solvers veranlasst hat - und es sieht so einfach aus )

[HowardMathis]

Your Sudoku-inspired rules sound interesting and exciting. I like the idea of filling a matrix with numbers, following certain rules for each area. It sounds like a fun challenge for the mind! I’m glad the game is already playable and a lot of fun. I’m sure it will appeal to a lot of people, especially those looking for a way to have a great time while waiting. It’s also great that it can be played under the guidance of a Tiwanaku game, which adds even more variety and variation.My advice is to keep exploring different approaches. It may be possible to try filling in the numbers according to the rules first and then see if such a background could be a solution. It is also worth considering other approaches and algorithms that can help optimize the process of creating levels.

[HowardMathis]

I already thought that there was a problem with the publication, I thought you would not approve the answer!

[Apo]

Tiwanaku ist immer noch in der Entwicklung.

Die aktuellste Version findet ihr immer hier:Tiwanaku

Ich habe mich weiter an die Erstellung der Levels gewagt und verschiedene Dinge ausprobiert.
Aktuell das beste Lösung für mich:

• weg von nur Untergrund erstellen und dann den Knuth Algo X draufhauen und schauen ob lösbar oder nicht
• hin zu
  • Erstellung des Untergrundes zufällig
  • eigene Prüfung spezieller Punkte, die ein Level unlösbar machen (3 einfache für jede Levelgröße - was zu einer Reduktion von nicht lösbaren Levels um ~70% geführt hat)
  • 2 weitere etwas komplexere Regeln, die überprüft werden für Levels größer als 5 x 5 sind. Diese dauern minimal länger, aber sorgen dafür, dass Knuth Algo X häufig nur aufgerufen wird, wenn das geht oder nur 1 bis 2 mal der Knuth zeigt, dass es nicht funktioniert
  • dauert trotzdem noch teilweise zu lange, da er zwar früher abbricht aber doch teilweise häufig neu erstellen muss.
  • Ziel muss es jetzt noch sein, die Erstellung des Untergrundes nicht nur zufällig zu gestalten, sondern auch Regeln zu finden, die das nächste Setzen eines Untergrundtiles schon nicht mehr so zufällig macht.

Es macht immer noch viel Spaß das Spiel im Meeting/im Bus/beim Warten auf zu haben. Ich habe auch das Feedback bekommen, dass es gerade durch dieses „Nebenbeispielen“ kein Problem ist, wenn die Levelerstellung 3 Sekunden dauert. Mich nervt es aber.