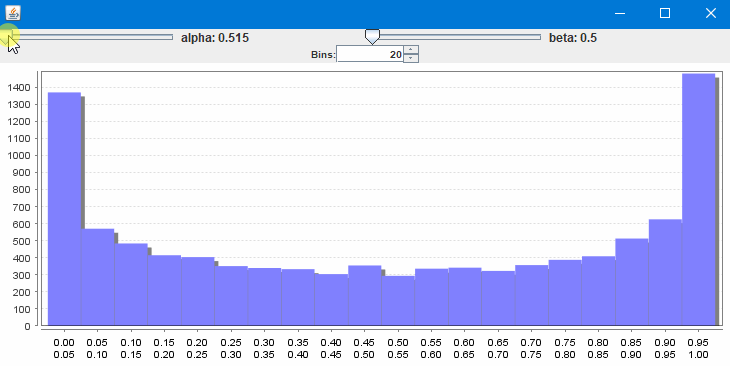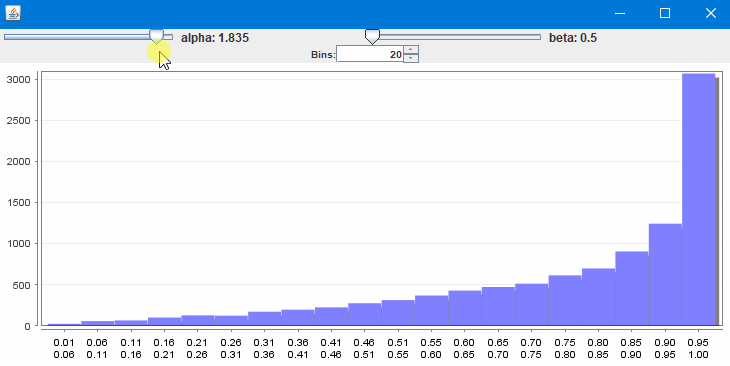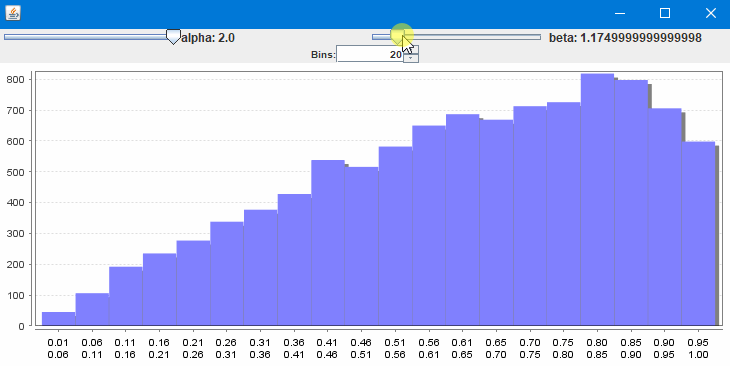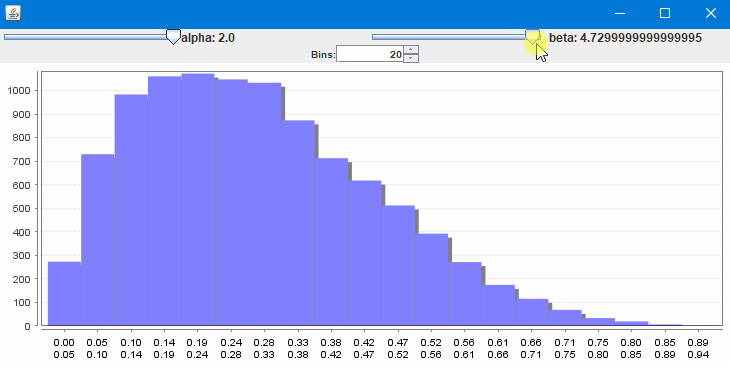
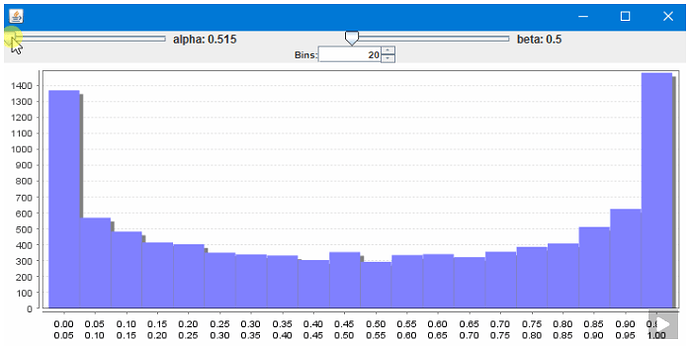
@Marco13 Entscheide du, was näher an der Parabelform wäre:
import org.apache.commons.math3.distribution.BetaDistribution;
import java.util.Arrays;
import java.util.Random;
import java.util.stream.IntStream;
public class Test1 {
private static final int n = 10000;
/**
* @param from lower bound
* @param to upper bound
* @param a factor between 0.0 and 1.0
* @return a random double value in bounds
*/
public static double getRandomDouble(double from, double to, double a) {
Random random = new Random();
double g;
do {
g = (random.nextGaussian() + 1.0) / 2.0;
} while (g < 0 || g > 1);
if (g < 0.5) {
g += (0.5 - g) * a * a;
} else if (g > 0.5) {
g -= (g - 0.5) * a * a;
}
return g * (to - from) + from;
}
public static double getRandomDouble2(double from, double to, double a) {
double v = new BetaDistribution(2, 2).sample();
if (v < 0.5) {
v += (0.5 - v) * a * a;
} else if (v > 0.5) {
v -= (v - 0.5) * a * a;
}
return v * (to - from) + from;
}
public static double f(int x) {
double x2 = (x - n / 2.0) / n;
double y = -x2 * x2 * 4 + 1;
return y * 2.0;
}
public static void main(String[] args) {
double[] a = IntStream.range(0, n).mapToDouble(i -> getRandomDouble(20, 30, 0)).toArray();
double[] b = IntStream.range(0, n).mapToDouble(i -> getRandomDouble2(20, 30, 0)).toArray();
double[] c = IntStream.range(0, n).mapToDouble(Test1::f).toArray();
int[] a2 = new int[10];
int[] b2 = new int[10];
int[] c2 = new int[10];
IntStream.range(0, n).forEach(i -> {
a2[(int) (a[i] - 20)]++;
b2[(int) (b[i] - 20)]++;
});
for (int i = 0; i < 10; i++) {
double sum = 0;
for (int j = 0; j < n / 10; j++) {
sum += c[i * (n / 10) + j];
}
c2[i] = (int) sum;
}
System.out.println("a2 = " + Arrays.toString(a2));
System.out.println("b2 = " + Arrays.toString(b2));
System.out.println("c2 = " + Arrays.toString(c2));
}
}
n=100:
a2 = [5, 10, 3, 11, 13, 14, 18, 12, 7, 7]
b2 = [5, 11, 7, 10, 15, 15, 14, 16, 3, 4]
c2 = [3, 9, 14, 18, 19, 19, 18, 15, 10, 4]
n=10000:
a2 = [814, 896, 1010, 1091, 1176, 1167, 1136, 1044, 903, 763]
b2 = [284, 760, 1128, 1395, 1447, 1478, 1335, 1121, 756, 296]
c2 = [372, 1013, 1493, 1813, 1973, 1973, 1813, 1493, 1013, 373]