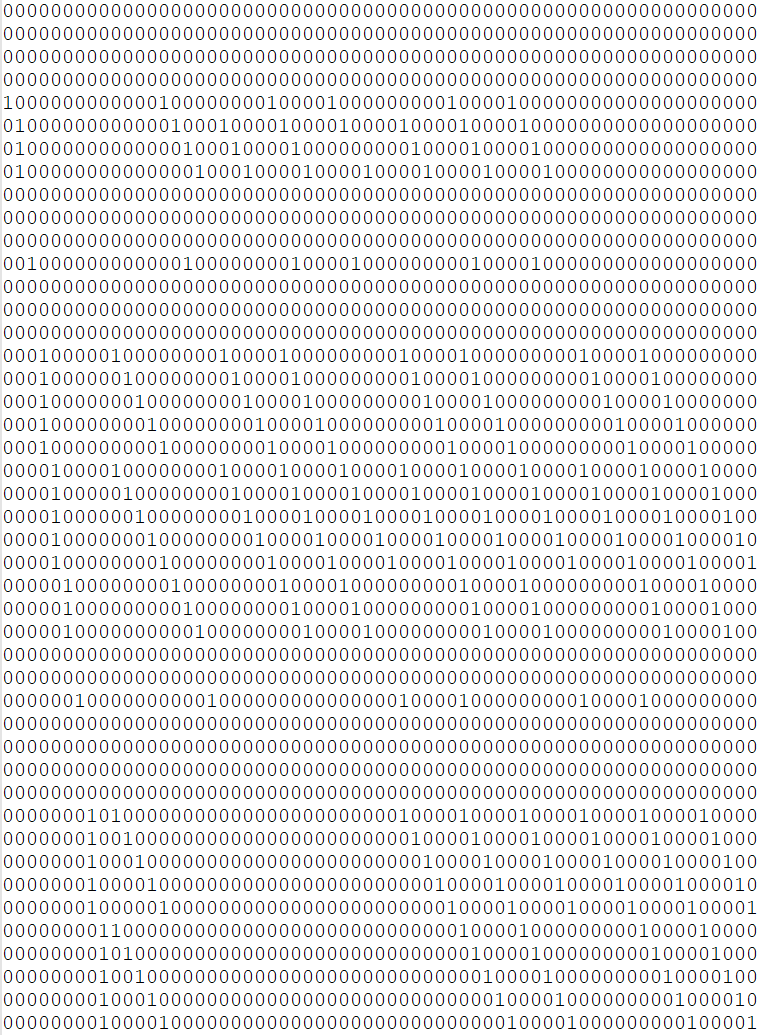Knuth's Algorithm X Frage

Apo · 24. April 2023 um 06:57

Hi,

Kurzfassung: Kann mir jemand bei der Erstellung der Binärmatrix zum Lösen eines Sudoku ähnlichen Problems mit Hilfe von Algorithm X helfen oder weiß, wo ich Fragen könnte?

Langfassung:
Wie einige wissen, erstelle ich ja gerne kleine 2d Logikspiele. Gerne auch Sudoku ähnliche Spiele. Also es gibt eine Matrix in der verschiedene Werte drin stehen und durch verschiedene Regeln kann die Matrix gelöst werden. Ob es nun Sudoku, Kakuro, Hitori etc heißt ist ja egal, alle haben das gleiche System im Hintergrund: Das Level wird nicht verschoben oder verändern, sondern nur durch Regeln gefüllt bis eine (in der Regel) eineindeutige Lösung herauskommt.

Jetzt bin ich wieder dabei so etwas zu erstellen und möchte natürlich alle Levels selber erstellen lassen. Dafür kann man ja den guten alten Brute Force Algorithmus nutzen oder seinen eigenen Algorithmus speziell für sein Problem zusammenstellen. Das ist in der Regel langsam und ineffizient. Dadurch habe ich mal geschaut, was es da schönes am Markt gibt. Und habe ich das Exact Cover Algorithmus gefunden (Exact cover - Wikipedia) und dazu die nette Variante von Knuth - Knuths Algorithm X gefunden (siehe Knuth's Algorithm X - Wikipedia ).

Nach einiger Zeit und mit Hilfe einiger netter Tutorials (Visualisierung: Exact Cover Visualizer und dazugehörige Beschreibung: GitHub - nstagman/exact_cover_sudoku: Exact Cover Sudoku Solver) habe ich ihn auch verstanden und für Sudokus selber umgesetzt. Da war ich glücklich. =)

Aber ich bekomme ihn für mein Problem gerade nicht umgesetzt.
Mein Spiel ist wie ein Sudoku. Eine Matrix, die mit Zahlen gefüllt werden muss.

Es gibt nur 3 Regeln:

Jede Zahl darf ich jedem Bereich nur einmal vorkommen. Das bedeutet in einem „Waldbereich“, welcher 5 Felder groß ist, müssen die Zahlen von 1 bis 5.
Im direkten Umkreis darf eine Zahl nur 1 mal vorkommen (das bedeutet wenn eine 2 in der Mitte steht, darf keine 2 in der direkten 8 Nachbarschaft (links, links oben, oben, rechts oben, rechts, rechts unten, unten, links unten) sein
Ein Bereich (wie z.B. Wald) darf sich nicht diagonal an einen weiteren gleichen Bereich angrenzen

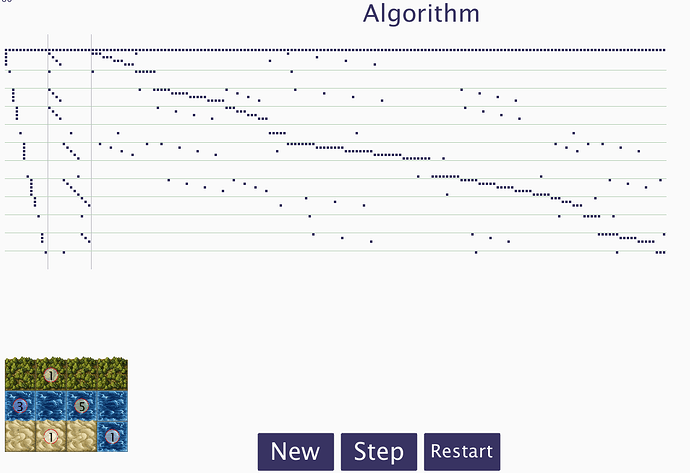
zur besseren Visualisierung (Ausgangslevel)

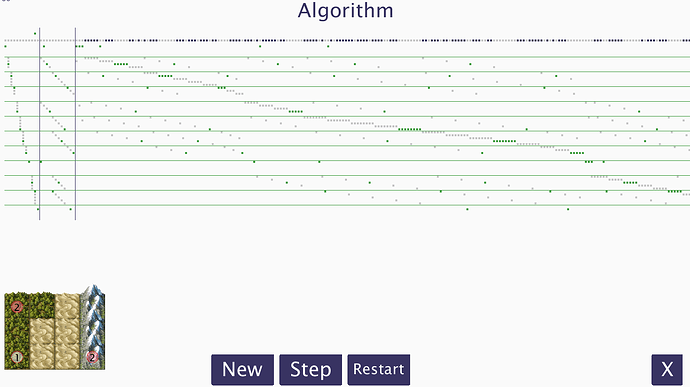
gelöstes Level mit den Regeln

Mein Problem jetzt ist, dass ich die direkte Nachbarschaft nicht in die binäre Matrix reinbekomme.
Die anderen Regeln sind kein Problem und funktionieren auch schon.
Was ist das Problem mit der direkten Nachbarschaft?
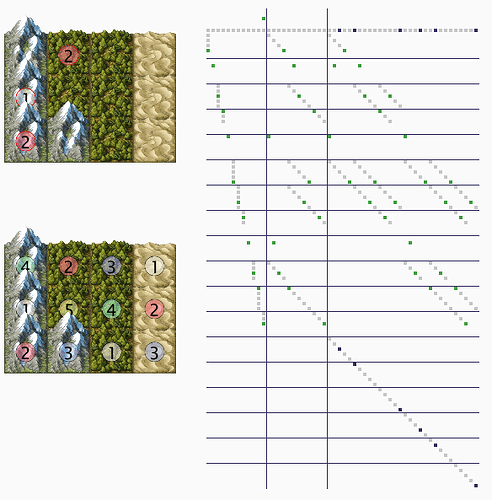
Perfektes Beispiel in der Mitte. In der Lösung steht die 4 und links und rechts davon die 3. Meine aktuelle Lösung hat das Problem, dass ich binär reinschreibe (ab Spalte 18) für Feld 0, 0 kann nur die 5 sein, also nur da die 1 aber das Feld daneben kann aktuell Werte 1 bis 5 haben also dafür die 1 rein usw … Das Problem dabei ist dass jetzt die mittlere vier mit links und rechts daneben stehenden Werten verbunden ist und somit wenn ich die drei setze, dann deselektiert er mir zwar die 3 in der Mitte, aber da die Mitte auch mit dem rechts daneben verbunden ist, tut er auch so als ob die 3 rechts mittig nicht mehr möglich ist. Das will ich aber nicht … ich weiß nur nicht wie ich es binär abbilde … kann mir da jemand helfen? Konnte ich das Problem so beschreiben, dass es überhaupt jemand verstanden hat?

Mein aktuelles binäres Array. Die Spalten 1 bis 9 repräsentieren die Möglichkeiten Zahlen reinzuschreiben, also Spalte 1 ist für Stelle oben links zuständig, da kennen wir die Zahl schon, also nur eine 1 an der 5 Stelle, da es eine fünf ist. In Spalte 2 (das Feld rechts neben der 5) ist unklar, aber kann nur die Werte 1 bis 3 beinhalten also werden sidn drei 1 zu sehen.
Die Spalten 10 bis 18 repräsentieren dass in einem Bereich nur 1 Zahl einmal vorkommen darf (also im Wasser nur die Zahlen 1 bis 3 und im Wald 1 bis 5 etc). Klappt auch wunderbar.
Nur die folgenden Spalten kriege ich nicht gelöst. =( Bitte helft mir =)

Marco13 · 24. April 2023 um 14:32

Von dem Algorithmus (und „Dancing Links“) habe ich mal gehört, aber IIRC nur auf der Ebene einer Präsentation, wo er mal an einem Trivialbeispiel durchgegangen wurde. Das kann zwar reichen, um ihn so weit zu verstehen, dass man ihn allgemein anwenden kann (so sind Algorithmen nun mal ) aber 1. ist das laaaange her, und 2. habe ich ihn sicher nicht so „tief“ verstanden, dass ich noch alle relevanten Punkte auf dem Radar habe, und 3. selbst wenn man sowas für eine Sache kennt, kann es sein, dass eine vermeintlich banale Abweichung von der ursprünglichen Problemstellung Anpassungen notwendig macht, die nicht offensichtlich oder trivial sind.

Letzteres bezieht sich grob darauf, dass man ein Problem ggf. transformieren muss. Hier ist das entscheidende wohl die Frage, wie man die constraints richtig in der Matrix repräsentiert. Und … ich vermute, du hast die Constraints nicht richtig modelliert.

(Leider kann ich nicht genau sagen, was daran „falsch“ ist, oder wie es „richtig“ wäre. Es ist nur eine Vermutung, und damit einerseits unfundiert-händewedelnd geraten, andererseits (da das der einzige Punkt ist, der bewirken kann, dass ~„der Algorithmus nicht ‚funktioniert‘“) vielleicht auch eine banale Offensichtlichkeit…)

Ich weiß nicht, ob ich konkret helfen kann, aber… bin an einigen Stellen gestolpert:

Ein Bereich (wie z.B. Wald) darf sich nicht diagonal an einen weiteren gleichen Bereich angrenzen

Das ist in dem Bild ja erstmal nicht so…?!

Das Problem dabei ist dass jetzt die mittlere vier mit links und rechts daneben stehenden Werten verbunden ist und somit wenn ich die drei setze, dann deselektiert er mir zwar die 3 in der Mitte, aber da die Mitte auch mit dem rechts daneben verbunden ist, tut er auch so als ob die 3 rechts mittig nicht mehr möglich ist.

Und das ist wohl der (händewedelnde) „Fehler in der Modellierung“:

Die Spalten 10 bis 18 repräsentieren dass in einem Bereich nur 1 Zahl einmal vorkommen darf

Es ist schwierig, auf diese Matrix draufzuschauen, und „zu verstehen“, wie genau dieser Constraint dort abgebildet ist. (Vielleicht würde es helfen, mal die Matrix für

 A A
 B B

zu sehen. Leider geht es nicht kleiner, und die Binärmatrix wird halt sehr schnell sehr groß und unübersichtlich…)

Es gibt da eine Frage, deren Antwort ich vielleicht „erarbeiten“ könnte, wenn ich laaaange über diesem Billd (!) einer Matrix brüten würde, die ich aber mal stelle - und sei es nur um als „Rubber Duck“ für dich zu dienen :

Wie genau ist die Tatsache modelliert, dass (für (row,col), 1-based) das Feld (1,1) ein Wald ist, und (1,2) ist Wasser, aber (2,1) ist wieder Wald? D.h. wie genau ist dort modelliert, dass zwischen (1,1) und (2,1) zwar ein Constraint existiert, aber zwischen (1,1) und (1,2) eben nicht?

Der Aussage …

da die Mitte auch mit dem rechts daneben verbunden ist

nach scheint das ja die Ursache für den Fehler zu sein…

Apo · 25. April 2023 um 21:37

Hi Marco,

du hast natürlich recht, dass das constraint falsch war, war mir bewusst. Ich wusste nur nicht wie ich es mache.

Ich hatte auf Arbeit mir einen armen Kollegen gesucht, der meine RubberDuck sein durfte. Er hat auch viel zum eigentlichen Verständnis des Algorithmus beigetragen. =)

Ich habe nun eine „mögliche“ Lösung gefunden, die funktioniert, aber etwas gegen die eigentliche binäreMatrix bzw. das ExactCover Problem geht.
Ziel ist es ja eine Matrix aufzubauen, die mir eine bestimmte Anzahl an Zeilen gibt, die komplett über alle Spalten eindeutig sind.
Mein Problem ist ja die Regel, dass die Nachbarn nicht die gleiche Zahl haben dürfen, aber in der 8er Nachbarschaft dürfen natürlich mehrere gleiche Zahlen vorkommen. Und das habe ich super schwer nur abbilden können. Das hat nun geklappt und ich „cheate“ dahingehend, dass ich nur alle anderen Constraints auswähle und überprüfe im Algorithmus. Durch das Rausstreichen, kommt die anderen Bedingung aber trotzdem zum Tragen. Dadurch ist der Algorithmus etwas langsamer, weil ich nicht nur Spalten mit der geringsten Anzahl mir aussuche, aber die eigentliche Bedingung ist ja vorhanden und löscht nicht machbare Lösungen. Das mag alles total verwirrend für euch sein (sorry dafür) und ich kann es schlecht beschreiben, aber es funktioniert nun. =) (Falls es er ausprobieren möchte, Alphaversion unter Tiwanaku )

Je größer das Level desto eher macht sich der Geschwindigkeitsvorteil gegenüber meiner eigenen Lösung bemerkbar (bei 9 x 5 Level um Faktor 100 ungefähr). Bei kleinen Level (3x3 oder 4x4) ist er aber teilweise sogar minimal langsamer als meine Lösung davor. Deshalb bin ich noch nicht perfekt zufrieden und werde weiter schauen, ob ich noch eine bessere/performantere Lösung finde.

Marco13 · 26. April 2023 um 01:16

Ja, das jetzt nachzuvollziehen (also die genaue Modellierung des Constraints in der Matrix) ist halt nicht einfach. Wie gesagt, ich hätte gedacht, dass man das Problem transformieren kann oder muss. Sinngemäß: Du hast ja im Moment einen Graphen

O-----O-----O
|\   /|     
| \ / |
|  X  |  ...
| / \ |
|/   \|
O-----O-----O
  ...

Und die „constraints“ entsprechen den Kanten. Und… ich hätte jetzt vermutet, dass man einfach Kanten weglassen kann. Nämlich alle Kanten zwischen Feldern (Knoten) die unterschiedliche Bilder haben.

Ansonsten … für „so eine Art von Problem“ kann man soweit ich weiß auch den AC-3 algorithm - Wikipedia verwenden, der ist IIRC recht leicht zu implementieren. (Ob er wirklich auf das Problem passt, müßte ich nochmal durchdenken, … wollte das jetzt nur mal als mögliches Keyword nennen)

Apo · 26. April 2023 um 08:55

Bei Knuths Algorithmus X will man ja einen Graphen haben, der alle Spalten genau einmal besucht hat. Ich habe es aber nicht hinbekommen die Spalten so zu füllen, das jede Spalte wirklich mindestens einmal ausgewählt wird.
Bei mir kann es vorkommen, dass alle Werte in einer Spalte „deselektiert“ für die Bedingung der Nachbarn werden, somit wäre die Size der Spalte bei 0 und der Algorithmus bricht ab. Das ist suboptimal und dadurch habe ich die Spalten so sortiert, dass alle anderen Constraints die ersten Spalten sind und die Überprüfung der Nachbarn am Ende. So kann ich einfach aufhören, wenn ich einen Graphen gefunden habe, der für die ersten Contsraints gilt. Da die anderen ja mit betrachtet werden, kommen auch nur valide Ergebnisse heraus. Der einzige Nachteil ist, dass ich ein Stück weit langsamer bin, da ich nicht immer die Spalte auswählen kann, die die wenigsten validen Elemente enthält.

Ich gebe noch nicht auf und werde es mal programmatisch visualisieren, damit ich vlt doch noch eine schöne Lösung hinbekomme. Ich glaube nicht, dass ich die einzige Person auf der Welt bin, die dieses Problem mit nicht eineindeutigen Werten in einer Zelle (durch die Nachbarn) hat. Da gibt es bestimmt schon etwas. =)

Zwecks AC-3 Algorithmus: Muss ich mal schauen, ob er mir noch besser passt. Danke. Den kannte ich auf jeden Fall noch nicht. =)

Marco13 · 26. April 2023 um 13:35

Ich muss/müsste 1. den Algorithmus in seiner Originalform noch mal durchgehen, 2. nachvollziehen, wie der auf dein Problem angewendet wurde (d.h. wie die Constraints in der Matrix genau codiert sind), 3. nachvollziehen, wie die den Algorithmus „verändert“ hast, und 4. (wichtig:) überlegen, ob der Algorithmus durch diese Änderung überhaupt noch „Algorithmus X“ ist (!)

Der letzte Punkt ist etwas kritisch. Wenn du (wie das jetzt ganz grob klang) bei dem Algorithmus einen Schritt veränderst, etwa von

"Wähle eine Zeile/Spalte der Matrix nach Kriterium X
zu „Wähle eine Zeile/Spalte der Matrix, die Bedingung Y erfüllt, nach Kriterium X“

dann kann das Auswirkungen auf die partielle/totale Korrektheit haben, die schwer vorherzusehen sind.

Oder anders: Stell dir vor, es gäbe eine existierende Implementierung (und natürlich gibt es die irgendwo), wo man einfach nur eine Methode wie

static Solution textbookVersionOfAlgorithmX(boolean matrix[][]) { ... }

aufruft, dann würde ich mir nicht viele Gedanken machen. Solange man es schaftt, sein Problem „richtig“ in diese matrix zu packen, ist alles gut.

Wenn man aber in seiner generischen AlgorithmX-Implementierung irgendwo eine Trennung zwischen boolean mainConstraints[][] und boolean differentFieldTypeConstraints[][] braucht, dann sieht das erstmal suspekt aus…

cmrudolph · 29. April 2023 um 07:25

Ich habe jetzt noch nicht alles im Detail durchgelesen, bin aber der Ansicht, dass sich das Problem auch auf Exact Cover zurückführen und dann mit DLX lösen lassen sollte. Ich verlinke dir mal ein anderes Beispiel, bei welchem ich auch DLX angewendet habe:

In der Readme habe ich die verschiedenen Constraints in Worten beschrieben. Vielleicht hilft das dabei noch einmal zu verinnerlichen, wie man ein Problem in Exact Cover überführt (das ist übrigens auch die eigentliche Komplexität dabei. Den Solver für das Legepuzzle habe ich von meinem Sudokusolver genommen und etwas angepasst)

Ich sehe mir dein Puzzle nochmal in einer ruhigen Minute an und versuche dann einen Vorschlag zu machen.

cmrudolph · 29. April 2023 um 08:39

Wenn ich das jetzt richtig verstanden habe (habe immer noch nicht alles gelesen), dann fehlt dir die Idee, um die direkte Nachbarschaftsbedingung zu formulieren.

Du kannst das so ähnlich machen, wie ich das auch bei bits&bytes gemacht habe, mit zusätzlichen, freien Matrixzeilen.

Stelle dir vor, dass auf jeder Kante und jeder Ecke eines zu befüllenden Feldes jede Zahl genau einmal stehen darf. Wenn du eine Zahl in ein Feld schreibst, sind alle Ecken und Kanten dieses Feldes mit der Zahl befüllt, die im Feld stehen. Weil die Eck- und Kantbedingungen sich mit den Nachbarfeldern geteilt werden, kann im Nachbarfeld keine gleiche Zahl mehr eingetragen werden. Nun ist aber das Problem, dass es ja ein Exact Cover Problem sein soll. Dazu brauchst du jetzt noch „freie“ Matrixzeilen, die es für jede Ecke und jede Kante gibt. Diese erfüllen genau eine Bedingung und füllen die fehlenden Zahlen auf.

Bei bits&bytes habe ich das so für die Nasen am Rand des Spielfeldes gemacht. Hier gibt es freie Zeilen, die ein Feld „ohne“ Nase modellieren, damit hier keine zu strikte Vorgabe für den Rand gemacht wird. Das kann man hier sehen: bitsandbytes/Puzzle.java at master · cm-rudolph/bitsandbytes · GitHub

Apo · 1. Mai 2023 um 11:38

Hi,

erst einmal danke @cmrudolph . Schaue ich mir doch gerne mal an.

Ich habe in der Zwischenzeit meine binäre Matrix visualisiert und selber zu verinnerlichen, wie ich ggf für mein Nachbarschaftsproblem vorgehen kann. (könnt ihr gerne selber ausprobieren unter Tiwanaku )

Unten links sieht man das Level, welches gelöst werden soll.
Die Matrix ist bei mir in 3 Contraints aufgeteilt (geteilt durch vertikale Linien).

Die ersten 12 Spalten sind für die Zahlen in den Zellen gedacht. Also die erste Spalte steht für links oben, aktuell leer dadurch 4 Möglichkeiten (ist in einem Biom mit der Größe vier). die zweite Spalte ist dann rechts daneben (in diesem Fall ein Wert 1 der bekannt ist und fest und dadurch in der Binärmatrix auch nur 1 Wert zu sehen in der Spalte) und so wird Zeilenweise durchgegangen für alle Zahlen.

Die Spalten 13 bis 24 zeigen das Constraint für die Regionen und wie sie zusammenhängen. (also in jedem Biom darf jede Zahl nur einmal vorkommen).

Die Spalten 25+ zeigen meine Idee von der Nachbarschaft. Die Zelle oben links hat 3 potentielle Nachbarn (rechts daneben, unten drunter und unten rechts). Deshalb ist für die erste Zelle es auch so kodiert, dass wenn wir die erste Zeile nehmen drei Spalten auf 1 gesetzt werden. Jede Spalte davon zeigt zu einem Nachbarn. So habe ich sichergestellt, dass sich nicht das Problem vom Threadanfang wiederholt. ABER ich habe das Problem, dass es dadurch Spalten gibt, die komplett deselektiert werden in Laufe des Algorithmus. Also ist mir schon klar, dass ich es nicht korrekt übersetzt habe, ABER es funktioniert, solange ich für die Auswahl welcher Wert in der Binärmatrix überprüft werden soll nur die ersten 2 Constraints genutzt werden. =)

Jetzt muss ich aber noch an die Erstellung des Untergrundes mit den verschiedenen Biomen gehen. Meine aktuelle Implemtierung ist zu langsam, dass sie fleißig ausprobiert ohne viel Logik. Dadurch kann es gerade in der Webversion dauern, bis eine Lösung gefunden wurde (was aber immer irgendwann passiert =) )

Apo · 1. Mai 2023 um 11:44

Eine Lösung eines Levels würde so aussehen. Und da sieht man auch für die dritte Bedingung gibt es Spalten die komplett deselektiert sind (grau) oder es kann vorkommen, dass es noch offene Spalten gibt.

Lesen kann man es aber so als Mensch:
Einfach die ersten 12 Spalten durchgehen. Eine Spalte steht für eine Zahl in einer Zelle.
Erste Zahl ist eine 2, die zweite ist eine 3 (also rechts daneben), die dritte eine 2, die vierte eine 1 usw. ausgewählt sind die grünen Punkte.

cmrudolph · 2. Mai 2023 um 05:10

Wieso werden bei deinem Ansatz Spalten komplett deselektiert? Das ist ja ein Anzeichen dafür, dass es sich dabei um keine gültige Lösung handelt.

Ich habe mir aber nochmal Gedanken über den „richtigen“ Lösungsansatz gemacht und habe festgestellt, dass mein voriger Vorschlag zu kompliziert war. Ich versuche nochmal den gesamten Aufbau der Matrix am 4x3 Spielfeld zu beschreiben. Die ersten 24 Spalten sind denke ich klar.

12 Spalten / Bedingungen: Zelle ist mit einer beliebigen Zahl befüllt
12 Spalten / Bedingungen: in jedem Biom kommt jede notwendige Zahl vor
30 Spalten / Bedingungen: in jedem Quadrant kommt jede mögliche Zahl vor

Zum letzten Satz an Bedingungen noch ein paar Worte. Mit Quadrant meine ich eine Gruppe von vier Zellen, die sich in einer Ecke berühren. Mit „jede mögliche Zahl“ meine ich die Zahlen 1 bis n, wobei n die höchstmögliche Zahl im Spielfeld ist. Also bei maximaler Biomgröße von 5 wäre n=5.

Da es 6 Quadranten und eine maximale Biomgröße von 5 gibt, ergeben sich hier 30 Bedingungen.

Nun zu den Zeilen der Matrix. Hier gibt es zwei verschiedene Typen.

In einem Feld steht eine bestimmte Zahl. Diese Zeilen erfüllen genau eine Bedingung vom ersten und eine Bedingung vom zweiten Typ. Außerdem erfüllen sie vom dritten Bedingungstyp diejenigen, bei welchen sie Teil des Quadranten sind (also maximal 4, hier im Beispiel maximal 2) und dessen spezifische Zahl sie darstellen. (insgesamt gibt es 60 Zeilen diesen Typs)
Auffüllzeilen: Diese Zeilen erfüllen keine Bedingung der ersten beiden Typen, sondern nur genau eine vom letzten Typ. Diese Auffüllzeilen gibt es für jeden Quadranten und jede Zeile (also genau 30 Stück).

Die Matrix hat insgesamt nur eine Größe von 54x90, was ziemlich klein ist. Die Lösung sollte vermutlich im Bruchteil einer Sekunde gefunden werden können (habe meine Solver lange nicht mehr laufen lassen, habe aber in Erinnerung, dass selbst viel größere Matrizen im Subsekundenbereich gelöst wurden).

Die Auffüllzeilen werden vom Algorithmus nur dann ausgewählt werden, wenn eine Spalte noch übrig ist und es keine anderen Zeilen mehr gibt, die diese erfüllen können. Das liegt daran, dass ansonsten nicht alle Bedingungen vom ersten und zweiten Typ erfüllt werden könnten.

Extraanmerkung: wenn du die Vorbelegung einer bestimmten Zelle mit einer bestimmten Zahl modellieren möchtest, vergrößerst du die Matrix um eine Spalte (du streichst also nichts weg). Diese Spalte ist eine zusätzliche Bedingung, die man „Zelle vorbefüllt“ nennen kann. Es gibt nur genau eine Zeile, die diese Bedingung erfüllen kann, nämlich die, bei der die entsprechende Zahl in der Zelle steht. Der Algorithmus wählt immer die Spalten mit den wenigsten Möglichkeiten aus und reduziert daher deine Matrix automatisch im ersten Schritt um die überflüssig gewordenen Zeilen.

Apo · 2. Mai 2023 um 07:24

Du hast Recht, das könnte gut klappen und die Idee mit den Quadraten und nicht der kompletten 8 Nachbarschaft spart sogar Spalten =).
Versuche ich sofort, auch das mit den Leerzeichen.

Ich denke mit der Idee der Leerzeichen klappt auch meine aktuelle Lösung.

Ich versuche beides und melde mich danach wieder. =) Danke

Apo · 2. Mai 2023 um 10:15

Es funktioniert! Durch die „Extrazeilen“ funktioniert der Exact Cover genau wie er sollte. Auch wenn sich die Extrazeilen komisch anfühlen, aber das war der fehlende Schlüssel.

Jetzt teste ich mal, ob es „Auswirkungen“ auf die Performance hat. Für das Lösen von einem 4 x 3 benötigt es in der Regel aber ~1 ms. Es wird erst interessant bei größeren Levels (9x5 z.B. da kam es vor der Änderung, wenn alle Lösungen gefunden werden sollten, dass es auch mal 3 Sekunden dauern konnte, da es über 400k an Möglichkeiten gibt, das teste ich heute Abend dann).

Ich lade heute Abend auch eine neue Version hoch.

cmrudolph · 2. Mai 2023 um 16:48

Magst du mal ein, zwei möglichst große Levels hier posten, gegen die ich meinen Solver mal als Benchmark laufen lassen kann?

Wenn ich das richtig verstehe nutzt du den Solver, um alle möglichen Lösungen zu finden, bei denen du dann nach und nach Zahlen einsetzt, bis die Lösung eindeutig wird?

Apo · 2. Mai 2023 um 20:29

@cmrudolph Möchtest du die Matrix oder ein Level mit der Struktur des Hintergrundes?

Also für folgendes Level habe ich 438.840 Lösungen in 1388450900 ns gefunden (also 1,3 Sekunden … das geht also noch schneller).

443334441
442344211
422111214
322411244
333442244

Jede Zahl steht für ein Biom.

Mein Problem ist auch, aktuell finde ich glaube ich noch doppelte Lösungen, muss schauen wie meine Abbruchbedingung für eine Lösung ist, damit es passt. Aktuell schaue ich, ob der Root Head auf sich selber zeigt als rechten Nachbarn und erstelle dann die Lösung.

Ich nutze den Solver, wie du richtig sagtest, um erst einmal alle Lösungen herauszufinden und dann nehme ich mir eine Lösung und erstelle daraus das eineindeutige Level (wo nur noch eine Lösung vorkommt).
Aber ich lösche am Anfang die Hälfte der Zahlen → falls nur eine Lösung dafür dann vorhanden ist, lösche eine zufällige weitere Zahl, falls dann wieder nur eine Lösung ist, lösche die nächste Zahl … usw.
falls mal mehr als eine Lösung vorkommt, kommt die letzte platzierte Zahl auf eine Blacklist (für die Anzahl der gelöschten Zahlen) und eine weitere wird gelöscht usw.
Da ich drei verschiedene Schwierigkeitsstufen habe, versuche ich unterschiedlich viele Zahlen zu löschen, aber immer ein Level zu haben, das genau 1 Lösung dann hat.

Ich habe auch die Webversion (Tiwanaku) geupdated und ergänzt, das man sieht, welche Zahlen er denkt in der Lösung zu haben.
Bsp:
Ausgangslage:

Zwischenschritt (mit falschen Annahmen):

Ergebnis:

cmrudolph · 3. Mai 2023 um 18:16

Als Struktur, also so, wie du das gepostet hast Ich weiß noch nicht, wann ich Zeit finde, das mal einzutickern - das wird vermutlich ja ein paar Stunden dauern, bis ich die Fachlichkeit um den Solver herumgebaut habe.

Nebenbei bemerkt: Algorithm X ist am schnellsten, wenn es wirklich nur eine Lösung gibt, oder wenn man bei der ersten Lösung abbricht. Ansonsten traversiert man doch recht viel vom Baum. Da du ohnehin nur an einer Lösung interessiert bist, wäre es vielleicht auch eine Möglichkeit, etwas Zufall in den Algorithmus einzubringen und bei Parität mehrerer Spalten eine zufällige auszuwählen.

Wie gehst du dann vor, wenn du die Lösung ausgedünnt hast? Lässt du dann nochmal den Algorithmus drüber laufen, oder vergleichst du einfach mit allen anderen gefundenen Lösungen? Ich würde schätzen, dass es am effizientesten wäre, die ausgedünnte Version zu nehmen und dann alle übrig gebliebenen Zahlen wie in meinem letzten Beitrag beschrieben als zusätzliche Spalten festzulegen und dann den Solver noch einmal laufen zu lassen, bis eine zweite Lösung gefunden wurde.

Apo · 3. Mai 2023 um 18:21

Die Idee mit dem Ausdünnen der vorhandenen Lösungen ist ja mal genial. Das versuche ich gleich.
Ich lasse aktuell mein eigenen Algorithmus (also eigentlich nur regelbasiert) jedes mal nach dem Setzen einer Zahl drüber laufen, der für das Finden einzelner Lösungen sehr schnell ist (wenn schon ein paar Werte drin sind).

Aber das Ausdünnen der Lösungen, die ich ja eh schon habe … die Idee ist super. Gerade wenn es vorher teilweise sortiert ist.

cmrudolph · 10. November 2024 um 18:45

Hat jetzt „etwas“ länger gedauert, bis ich das mit dem Beispielpuzzle einmal implementiert habe.

Ich habe mich noch einmal mit Algorithm DLX beschäftigt und dabei ist eine wiederverwendbare Java-Lib herausgefallen, die ich auch in maven central veröffentlich habe (Maven Central: de.famiru.dlx:dlx). Den Quellcode und die Readme findet man im github-Repository.

Der oben verlinkte Beispielcode aus meinem Bits-and-Bytes-Solver entspricht nicht dem Algorithm DLX - vermutlich habe ich mich da aus einer Sekundärquelle bedient… Nachdem ich das Original-Paper noch einmal intensiv studiert habe, entspricht der Code jetzt auch wirklich Algorithm DLX, kann auch generalisierte Exact Cover-Probleme lösen (also mit Bedingungen, die maximal einmal erfüllt sein dürfen) und ist deutlich performanter.

Das Tiwanaku-Problem ist übrigens auch ein generalisiertes Exact Cover-Problem. Die dritte der von mir aufgeführten Bedingungen darf maximal einmal erfüllt werden. Deshalb hatte ich vorgeschlagen, Pseudo-Zeilen in die Matrix einzufügen. Wenn man das direkt als verallgemeinertes Problem betrachtet, wird die Matrix aber deutlich kleiner. Auf meiner Maschine dauert das Lösen nur ca. 270ms. Dabei kommen ebenfalls 438.840 Lösungen heraus. Ich glaube nicht, dass da doppelte Lösungen bei sind.

Den Solver kannst du hier finden: GitHub - cm-rudolph/tiwanaku: Tiwanaku solver

Apo · 11. November 2024 um 16:04

Vielen Dank. <3

Auf meinem Arbeitsrechner ist deine Lösung ungefähr 6 mal schneller. Schaue ich mir noch einmal später in Gänze an, was anders ist. Erkenne sehr viel auf dem ersten Blick aber grundsätzlich wieder. Schneller ist aber immer besser =)

Dein Code nutzt Java 1.16+ Features, sodass ich es noch einmal minimal umschreiben muss, damit es bei mir funktioniert (für libgdx und die Nutzung von GWT 2.8 für die HTML Version benötige ich Java 1.8).

Aber noch einmal vielen Dank für deine Antwort. <3

€dit: ok, das Umschreiben war easy, war wirklich nur der record. Es funktioniert super und ist immer noch genau so schnell. Ich bin begeistert. Vielen Dank!

cmrudolph · 11. November 2024 um 19:10

Ich hatte auf Java 17 basiert, da ich davon ausging, dass neuere Projekte keine so alten Java-Versionen mehr nutzen. Und da Java 17 die älteste noch unterstützte LTS ist, hatte ich die records „mitgenommen“. Würde dir eine jdk8-Version bei maven central helfen? Wie du schon richtig gesehen hast, ist es kein größerer Aufwand, das umzubauen.

Edit: Habe es einfach mal released. Es gibt jetzt eine Version 0.6.1-jdk8.